>>>>>>> Yes, I already noted that you view discussing physics as some kind of
>>>>>>> wrestling match where the objective (at least in your eyes) is to
>>>>>>> vanquish your opponent...
>>>>>> I do.
>>>>> Why?
>>>> The answer is very simple. IT CANNOT NOT EXPLAIN THE TWIN PARADOX.
>>>> This is not experimental evidence. It is mathematical and logical
>>>> evidence. Yes, you fumbled through the standard paradox, but
>>>> relativity has no answer for the David Variation. Now you claim you
>>>> have answered it (reply TYPE#3 in the con artist repertoire), but
>>>> where is it? Is it in some secret vault? Yes you mentioned something
>>>> about a twin being older, but a claim is not mathematical proof.
>>>> Where is your calculation?
>>>>
>>>> Now, the counter claim is that SR/GR has experimental backing.
>>>> Where? I just demolished all evidence against SR/GR as weak and
>>>> circumstantial. You could not even defend the HK weakness, the PR
>>>> weakness, the lack of LIGO evidence, the lack of GP evidence, the wide
>>>> error margins of the PPO of earth, and so on. The red shift and light
>>>> bending may be explained by GR, but it is equally and better explained
>>>> by entropy and refraction. So you see, when push comes to shove, SR/
>>>> GR has no solid backing. But wait, let us go to the underlying
>>>> logic. It is fallacious. Why? Why? Why? because it results in the
>>>> irreconciliable twin fallacy. Now, if you want to convince anyone
>>>> that you have answered the David Twin paradox, post it RIGHT NOW! But
>>>> you cannot. Because there you have no resolution.
>>>>
>>>> You have been bluffing and your bluff has been exposed. RELATIVITY
>>>> CON ARTISTS using tricks up their sleeve to dodge the question. But
>>>> I'm sticking it to your face. Oh, yes, you won't be dared. Yeah
>>>> right. If you had the answer, you'll stick it to my arrogant face
>>>> right now. But you can't right? So here I am, STRICH, the arrogant
>>>> bastard, who shamed all the Relativity Con Men, who can't be silenced,
>>>> because, the only thing that will silence the question, is the answer,
>>>> which you never had, do not have, and will never have, because ILLOGIC
>>>> has no answer.
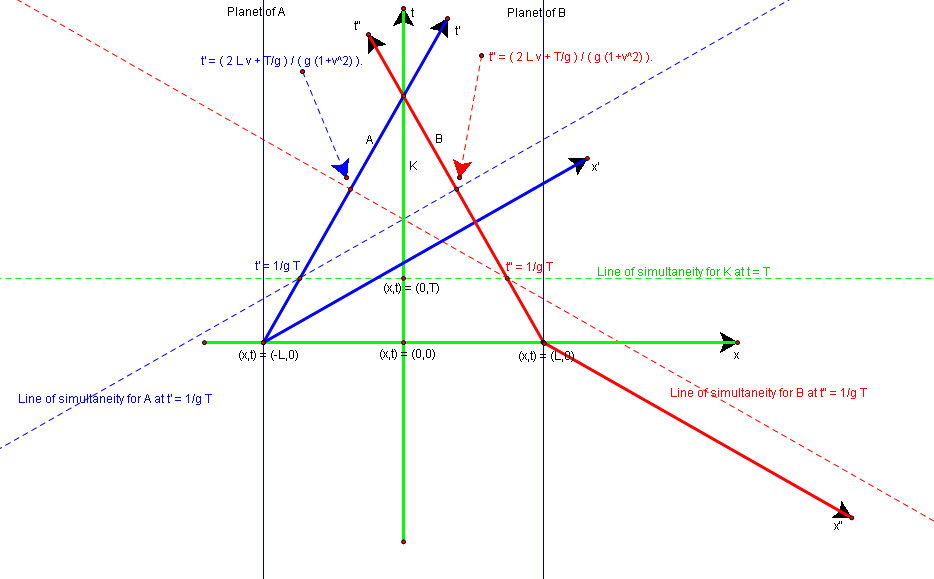
>>> Inertial system K using coordinates x and t.
>>> Twin A is on planet at x = -L and uses coordinates x' and t'.
>>> Twin B is on planet at x = L and uses coordinates x" and t".
>>> In system K the twins have the same age 0 at time t = 0.
>>>
>>> At event (x,t) = (-L,0) twin A suddenly moves with velocity v towards
>>> x = 0 at his event (x',t') = (0,0).
>>> At event (x,t) = (L,0) twin B suddenly moves with velocity -v towards
>>> x = 0 at his event (x",t") = (0,0).
>>>
>>> We use units where c = 1 (so -1 < v < 1) and abbreviate
>>> g = 1/sqrt(1-v^2).
>>>
>>> Lorentz transformation [LTA] between K and A is
>>> { x' = g ( x+L - v t )
>>> { t' = g ( t - v (x+L) )
>>> and the inverse [LTAi]
>>> { x+L = g ( x' + v t' )
>>> { t = g ( t' + v x' )
>>>
>>> Lorentz transformation [LTB] between K and B is
>>> { x" = g ( x-L + v t )
>>> { t" = g ( t + v (x-L) )
>>> and the inverse [LTBi]
>>> { x-L = g ( x" - v t" )
>>> { t = g ( t" - v x" )
>>>
>>>
>>> 1) Looking from K:
>>> Wordline (equation of motion) of origin of K:
>>> x = 0
>>> Wordline (equation of motion) of twin A:
>>> x+L = v t
>>> Wordline (equation of motion) of twin B:
>>> x-L = -v t
>>> Time of arrival at home at x = 0 for both twins:
>>> t = L/v
>>> Home arrival event H for both twins
>>> (x,t) = (0,L/v)
>>> Age of twin A at some time t = T is t'-coordinate of solution of
>>> { x' = 0
>>> { T = g ( t' + v x' )
>>> giving
>>> t' = 1/g T
>>> Age of twin B at some time t = T is t"-coordinate of solution of
>>> { x" = 0
>>> { T = g ( t" - v x" )
>>> giving
>>> t" = 1/g T
>>> Conclusion, in K, at any time t = T, the twins A and B have
>>> the same age 1/g T.
>>>
>>>
>>> 2) Looking from A at event where A has age t' = 1/g T
>>> i.o.w. at event ( x', t' ) = ( 0, 1/g T )
>>> i.o.w. with [LTAi] at event ( x, t ) = ( -L + v T, T )
>>> Line of A-simultaneity in K-coordinates:
>>> x - (-L + v T) = 1/v (t - T)
>>> Worldline of B in K-coordinates:
>>> x-L = -v t
>>> Point of A-simultaneity on worldline of B by solving
>>> the previous 2 equations for x and t
>>> { x = ( (L- v T)/g^2 )/(1+v^2)
>>> { t = (T/g^2 + 2 L v)/(1+v^2)
>>> Transforming to B-frame to find age t" of B and verifying
>>> that x" = 0:
>>> { x" = 0
>>> { t" = ( 2 L v + T/g ) / ( g (1+v^2) )
>>>
>>> So, when A has age t' = 1/g T, then according to A, his twin
>>> brother B has age t" = ( 2 L v + T/g ) / ( g (1+v^2) ).
>>> Let's see what happens when they meet at T = L/v:
>>> t' = 1/g L/v
>>> t" = 1/g L/v
>>> which is the same age.
>>> According to A, his brother B is older, but aging slower in
>>> such a way that they have the same age when they meet.
>>>
>>>
>>> 3) Looking from B at event where B has age t" = 1/g T
>>> i.o.w. at event ( x", t" ) = ( 0, 1/g T )
>>> i.o.w. with [LTBi] at event ( x, t ) = ( L - v T, T )
>>> Line of B-simultaneity in K-coordinates:
>>> x - (L - v T) = -1/v (t - T)
>>> Worldline of A in K-coordinates:
>>> x+L = v t
>>> Point of B-simultaneity on worldline of A by solving
>>> the previous 2 equations for x and t
>>> { x = ( (-L+ v T)/g^2 )/(1+v^2)
>>> { t = (T/g^2 + 2 L v)/(1+v^2)
>>> Transforming to A-frame to find age t' of A and verifying
>>> that x' = 0:
>>> { x' = 0
>>> { t' = ( 2 L v + T/g ) / ( g (1+v^2) )
>>>
>>> So, when B has age t" = 1/g T, then according to B, his twin
>>> brother A has age t' = ( 2 L v + T/g ) / ( g (1+v^2) ).
>>> Let's see what happens when they meet at T = L/v:
>>> t" = 1/g L/v
>>> t' = 1/g L/v
>>> which is the same age.
>>> According to B, his brother A is older, but aging slower in
>>> such a way that they have the same age when they meet.
>>>
>>>
>>> Dirk Vdm
>> Nice try Dirk. Only analyses (1) is correct as you used a frame K at
>> rest in the middle of twins A and B. Your analyses (2) and (3) still
>> used the same frame K, while purporting to analyze from A and B
>> respectively.
> Haven't you learned how to eliminate variables from systems
> of equations in your highschool linear algebra courses?
>> Now either you are stupid and did the wrong analyses,
>> or you think we are stupid and such a glaring error will not be easily
>> seen. Have you forgotten your RELATIVITY?
> Analysis (2) used frames K and A with the Lorentz Transformation
> between them.
> Analysis (3) used frames K and B with the Lorentz Transformation
> between them.
> Although this is a standard technique, used as from page 3 in
> introductory courses on special relativity, perhaps you haven't
> heard of it. That would not surprise me.
>
> Since according to linear algebra the Lorentz transfomations form
> a group, these analyses are valid. But perhaps you think you have
> some experimental evidence for the invalidity of linear algebra.
> That would not surprise me either. Feel free to share it with us.
>> Let me show you how to do a CORRECT second analyses from the A frame.
>> A is at coordinate (x, t) = (0,0) and B is at (x,t) = (D, 0) where
>> D=2L. More importantly, for A, velocity=0, and for B, velocity=V
>> where V can be simply V=v+v for small velocoties.
> So, feel free to provide the complete analysis, and compare
> with mine. Don't forget to show every detail of your calculation,
> so I can help you when you get stuck.
> Don't forget that we are talking about arbitrary velocities and we
> are working in special relativity, so make sure you take
> V = 2 v/(1+v^2)
> - you probably recognise this quantity in the expressions:
> ( 2 L v + T/g ) / ( g (1+v^2) )
>
> In order not to get stuck, I advise you to use the same variables
> As I have, namely (x',t') for A and (x",t") for B.
> This way you can verify what happens if you manage to
> eliminate variables x and t from [LTA] and [LTB] and compare
> with you find.
>
> Dirk Vdm
CRAP
|