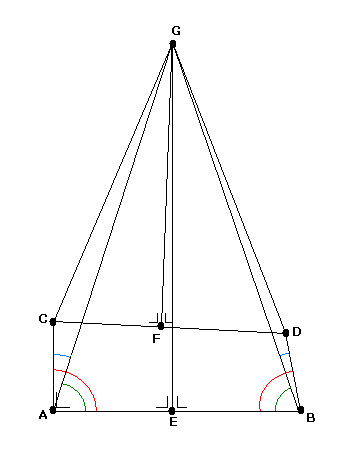
A proof by construction
Where is the error?
Apparently this 'proof' was created by Lewis Carroll.

Draw a horizontal
line AB,
Draw AC perpendicular to AB,
Draw BD such that BD is not
perpendicular to AB, but such that |CA| = |BD|,
then point D is
'below' point C.
Put point E in the middle of AB,
Put point F in the middle of CD,
then point F is on
the left of point E,
Draw a line through E perpendicular
to AB,
Draw a line through F perpendicular
to CD,
then these lines
cannot be parallel and intersect in a point G
By construction we have
angle(EAG) =
angle(EBG)
[1]
We already know that
|CA| = |BD|
By construction we have
|AG| = |BG| ( because E is in the middle of
AB and EG perpendicular to AB )
|CG| = |DG| ( because F is in the middle of
CD and FG perpendicular to CD )
So the triangles (ACG) and (BDG) are
congruent, therefore
angle(GAC) =
angle(GBD)
[2]
But we had
angle(EAG) +
angle(GAC) =
angle(EAC) = 90 degrees
[3]
and
angle(EBG) +
angle(GBD) =
angle(EBD) < 90 degrees
[4]
From [1], [2] and [3], we have
angle(EBG) +
angle(GBD) =
angle(EAC) = 90 degrees
[5]
So from [5] and [4] we have
angle(EAC) =
angle(EBD)
and so finally
90 degrees < 90 degrees ;-)
Hit this to mail me.
(-: Dirk Van de moortel ;-)