Het rechthoekvrije rooster



Een vierkant van 2 bij 2 kunnen we vierkantvrij maken door minimaal 3 (volgens Vierkantvrij: het aantal zwarte vierkantjes + 1) lijnstukjes van lengte 1 te verwijderen. Daarbij wordt ook een lijstukje op de rand van het grote 2x2 vierkant weggehaald.


In de eerste figuur ziet u zo'n 2x2 vierkant. Zijde a wordt weggehaald. Nu is het (op één manier) mogelijk om in totaal 3 lijnstukkjes weg te halen en een rechthoekvrije figuur over te houden (zie rechthoek ABCD).


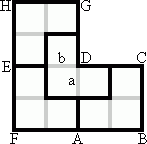
Spiegel vierkant ABCD om AD. Dat levert rechthoek FBCE. Nu is rechthoek FBCE nog in tact, dus moet een van de randlijnstukjes van FBCE worden verwijderd. Kies daarvoor lijnstukje b. Dat is handig, want nu kunnen we vierkant FADE spiegelen om ED en hoeven dan geen extra lijnstukje te verwijderen.
Kortom een L-tromino met lange zijde 4 is rechthoekvrij na verwijdering van minimaal 8 lijnstukjes.


In de laatste figuur wordt een overdekking getoond met 5 grote L-tromino's (met lange zijde 4). Van het overblijvende vierkantje met zijde 2 moeten nog 3 lijstukjes worden afgepakt. In totaal moeten dus minimaal 43 lijnstukjes worden verwijderd.

Op een dambord (10 bij 10) moeten 55 lijnstukjes worden verwijderd. (Voor de lezer).