Het domino probleem (deel 3)

Als we één zwart veld willen verwijderen, dan is een bedekking snel gevonden. Zie het volgende plaatje voor een hint.


We bekijken nu het probleem waarbij 3 velden worden verwijderd.
We zullen veel meer aantonen. Daardoor wordt het probleem minder star, zodat je gebruik kunt maken van volledige inductie.
We tonen aan dat je elk rechthoekig 2k+1 bij 2m+1 bord met k>0 en m>0 volledig kunt bedekken als je er 2 zwarte velden en 1 wit veld uit hebt verwijderd.
De bewering is juist voor k=1, m=1. Zie hiervoor de plaatjes


Bekijk nu een 2K+1 bij 2M+1 rechthoek met KM>1 en veronderstel dat de stelling al bewezen is voor kleinere rechthoeken.
Markeer langs de langste zijde twee stroken van breedte 2 aan beide uiteinden van de rechthoek (zie figuur).


Een van de uiteinden bevat 0 of maximaal 1 verwijderd veld, zeg uiteinde A.
Geval 1: A bevat geen verwijderde velden. Dan bevat de rechthoek zonder A 3 verwijderde velden en volgens de inductieveronderstelling kan dat gebied volledig met domino's worden bedekt. Dat geldt ook voor strook A zelf (stapeltje domino's van breedte 2).
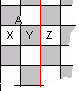
Geval 2: A bevat 1 verwijderd veld. Stel het is veld X (zie tekening). Als we in de rechthoek zonder strook A ook nog veld Z verwijderen, dan is volgens de inductieveronderstelling die rechthoek zonder strook A en zonder de 3 verwijderde velden volledig met domino's te overdekken.
Bedek nu strook A volledig met horizontaal geplaatste domino's en schuif domino XY een plaats naar rechts. We hebben dan onze bedekking gevonden met veld X verwijderd uit A.
Stel veld X was niet een wit, maar een zwart veld en veld Z was een van de verwijderde velden. Dan bevat strook B 0 of maximaal 1 (wit) verwijderd veld. We moeten dan niet uitgaan van strook A maar van strook B.


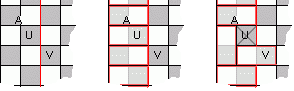
Tot slot. Stel A bevat 1 verwijderd veld in de tweede kolom. Zeg het is veld U (zie tekening). Verwijder nu even ook veld V. Dan kan de rechthoek zonder strook A en zonder de verwijderde velden volledig worden overdekt. Zie dan in de laatste 2 plaatjes hoe veld V door veld U kan worden vervangen.
Hiermee zijn alle gevallen besproken en is het bewijs rond.