Het domino probleem (deel 4)

Er zijn 10 mogelijke doorsnijdingen, 5 horizontale en 5 vertikale.
Elke doorsnijding verdeelt het bord in 2 rechthoeken met een even aantal velden (immers zo'n rechthoek heeft óf lengte 6 óf breedte 6).
Een doorsnijding kan niet precies één domino halveren, want dan ontstaan er rechthoeken met een oneven aantal velden.



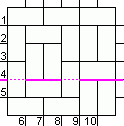
(Bewijs: Stel, een doorsnijding halveert precies 1 domino. Dan ontstaan 2 rechthoek die bedekt zijn door "een geheel aantal domino's + een halve" en "een geheel aantal domino's + een halve" bedekken een oneven aantal velden.)
Dus als elke doorsnijding een of meer domino halveert, dan doorsnijden de 10 lijnen minstens 20 domino's.
Dat is onmogelijk, want een 6 bij 6 bord wordt bedekt door 18 domino's, en elke domino wordt door precies 1 doorsnijding doormidden gedeeld.
Dus er is altijd een doorsnijding die geen enkele domino halveert.