Koppelingsanalyse

Om er zeker van te zijn dat ons genetisch verhaal ook voor de minder genetisch onderbouwden helder is, volgt hieronder een korte bespreking over wat nu precies een LOD-score is. Het betreft hier een lichte bewerking van de tekst die wij zelf ook gebruikten om dit fenomeen te doorgronden. Omwille van de uitermate sterke didactische opbouw hebben wij er niet teveel aan gesleuteld en enkel hier en daar wat anders bewoord en ingekort.

Inleiding
Wanneer genetische kenmerken louter afhankelijk zijn van één locus dan is deze mendeliaans. Hierbij komen we dan tot de overervingsmogelijkheden autosomaal dominant (AD), autosomaal recessief (AR), geslachts(X)-gebonden dominant of geslachts(X)-gebonden recessief.
Indien een genetisch kenmerk niet mendeliaans is, dan is deze multifactorieel, oftewel bepaald door een combinatie van genetische en omgevingsfactoren en hoeft dus niet door een enkele locus bepaald te worden.
Met behulp van koppelingsanalyse kan men kwantitatief bepalen of een kenmerk bepaald wordt door één enkele locus die in de nabijheid ligt van andere reeds gekende loci op een genoom en tevens de afstand hiertoe. Zo kan men dan het kenmerk op de genetische kaart van het genoom zetten

Enkele definities en principes
locus: fysische plaats op een chromosoom. Op een locus bevindt zich een bepaalde sequentie of gen. Een locus draagt een specifiek allel van dit gen.
allel: een van de alternatieve vormen van een gen op een bepaald locus.
genetische marker: elk locus kan gebruikt worden als genetische marker van zodra het mogelijk is genetische variatie ter hoogte van dit locus te detecteren.
haplotype: in een strikte betekenis, de specifieke allelen van verschillende loci die zich op dezelfde fysische chromosoom bevinden. In de brede betekenis zeggen we dat een set allelen voor verschillende loci een haplotype vormen. We erven dan een haplotype van onze moeder en een haplotype van onze vader.
genotype: genetische constitutie van een organisme. Ons genotype wordt gedefinieerd door twee specifieke allelen voor elke locus.

Normaalgesproken is er sprake van onafhankelijke segregatie van allelen, dus onafhankelijke overerving. Voor twee markers met als allelen respectievelijk A, a en B, b zijn de mogelijke haplotypes van de gameten: AB, Ab, ab en aB. Deze worden in een ratio 1:1:1:1 doorgegeven aan de nakomelingen.
Sommige paren van genen worden niet onafhankelijk overgeërfd, deze genen zijn gekoppeld. Veronderstellen we een individu met als haplotypes AB en ab voor twee loci zoals hierboven beschreven. Erven nakomelingen van dit individu het AB of het ab haplotype, dan noemen we deze niet-recombinant voor deze twee loci. Nakomelingen die een Ab of aB haplotype erven van deze ouder hebben een recombinant haplotype. Segregeren deze twee genen niet onafhankelijk, dan zullen de niet-recombinante haplotypes voor deze twee genen frequenter voorkomen bij de nakomelingen dan de recombinante haplotypes. De allelen van beide genen overgeërfd van één ouder zijn dan schijnbaar gekoppeld, zij het niet absoluut. Dit fenomeen heet genetische koppeling (genetische linkage). Kwantitatief wordt koppeling gemeten als de recombinatiefractie q, de verhouding recombinanten/niet-recombinanten. Dit is ook de waarschijnlijkheid dat een bepaalde ouder een recombinant haplotype doorgeeft aan een kind. Loci die onafhankelijk overerven zijn niet gekoppeld. De geobserveerde recombinatiefractie is dan q =½. Zijn twee loci volledig gekoppeld, dan komen er geen recombinanten voor en q = 0.
Deze definitie van koppelingsanalyse heeft drie belangrijke gevolgen:
a) koppelingsanalyse vereist onderzoek van verwante individuen, niet verwante individuen zullen geen informatie opleveren.
b) recombinante en niet-recombinante haplotypes kunnen niet altijd onderscheiden worden. Stel dat een persoon een Ab/ab genotype bezit (de twee haplotypes zijn dan Ab en ab). Omwille van de homozygositeit van de tweede locus (genotype b/b) kan men de recombinante haplotypes afkomstig van dit individu niet onderscheiden van de niet-recombinante haplotypes. Om dit onderscheid te kunnen maken moet een persoon dus heterozygoot zijn voor beide loci. Dan alleen is een individu informatief voor koppelingsanalyse.
c) een Ab haplotype is recombinant als het afkomstig is van een AB/ab individu en niet-recombinant als het voortkomt van een individu met Ab/aB genotype. Deze twee mogelijkheden voor een dubbele heterozygoot moeten dus onderscheiden worden (met andere woorden, een persoon met haplotypes Ab en aB moet onderscheiden worden van een persoon met haplotypes AB en ab). De specifieke haplotypes die voorkomen bij een dubbele heterozygoot worden ook fase genoemd.

Homologe recombinatie
Gameten ontstaan uit diploïde kiemcellen door meiose. Tijdens dit proces kan genetisch materiaal uitgewisseld worden door homologe recombinatie of crossing-over. Zo worden dus de recombinante haplotypes gegenereerd. Dergelijke crossing-over kan overal op een chromosoom plaatsgrijpen. De kans dat dit voorkomt tussen twee loci die op één chromosoom liggen is dus veel kleiner als deze dicht bijeen liggen dan wanneer zij ver van elkaar verwijderd zijn. Er is dus een verband tussen de fysische en de genetische afstand die twee loci scheidt. De recombinatie fractie q wordt ook uitgedrukt in centiMorgan (cM): 1 cM komt overeen met 1% recombinatie. Gemiddeld komt 1% recombinatie overeen met 10⁶ bp (1 mb). Hier kunnen lokaal echter grote verschillen optreden: op specifieke plaatsen van het menselijk genoom kan 1% recombinatie overeenstemmen met 5 . 10⁴ bp, op andere met meerdere mb.
In het algemeen is er meer recombinatie aan de uiteinden van de chromosomen dan rond de centromeer. Recombinatie is ook frequenter in de vrouwelijke meiose dan in de mannelijke meiose. Er zijn dus vrouwelijke en mannelijke genetische kaarten. Voor de meeste toepassingen wordt hiervan een gemiddelde genomen.

Kwantitatieve methodes
Het hoofdprobleem bij de constructie van een genetische kaart van de mens is de bepaling van de meest waarschijnlijke reële recombinatiefractie uitgaande van een beperkt aantal observaties in families. Stel dat we binnen één familie de overerving van twee merkers analyseren en een aantal recombinaties waarnemen. De vraag is nu wat deze waarneming ons leert over de reële recombinatiefrequentie tussen de twee merkers, en met welke statistische zekerheid. Het is immers mogelijk dat de gemeten recombinatie frequentie in de familie afwijkt van gemiddelde 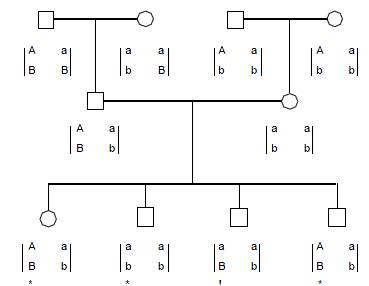recombinatie frequentie tussen de twee merkers in de populatie. Beschouwen we de overerving van twee merkers de 3-generatie familie uit nevenstaande stamboom. De vader is dubbel heterozygoot voor beide merkers en dus informatief. De haplotypes van de vader (of de fase) kunnen bepaald worden door de genotypes van zijn ouders te analyseren. De moeder is homozygoot voor beide merkers en dus niet informatief. Er zijn dus vier informatieve chromosomen (preciezer: meioses), drie niet-recombinanten (*) en één recombinant (!). De geobserveerde recombinatiefrequentie tussen de merkers A en B binnen deze familie is dus 0,25. Het is echter duidelijk dat als wij de hele populatie zouden onderzoeken de gemiddelde recombinatiefrequentie tussen de twee merkers dan merkelijk zou kunnen verschillen van de waarde in die familie, omdat recombinatie een toevallig proces is.
Er is dus behoefte aan een statistische methode om, uitgaande van deze experimentele waarnemingen, de gemiddelde of reële recombinatiefractie te bepalen tussen merkers, en een idee te krijgen over de statistische zekerheid waarmee wij die uitspraak kunnen doen. De meest gebruikte statistische methode voor koppelingsanalyse is de lod score (logarithm of odds) methode. L(q) wordt gedefinieerd als de probabiliteit dat we een waarneming doen in een experiment (familie) als de reële gemiddelde recombinatiefractie q is (gekoppelde merkers). De wijze waarop L(q) wordt berekend is dus afhankelijk van de structuur van de familie die we analyseren. De waarschijnlijkheid dat er bij één meiose recombinatie optreed is q. De waarschijnlijkheid dat erbij één meiose geen recombinatie optreed is dus (1-q). In deze familie is zijn vier informatieve meioses. Bij één van deze vier meioses trad er recombinatie tussen de merkers op. Voor deze waarneming is L(q) = (1-q)³q
Vervangen wij in die formule q door 0,5 (recombinatiefractie 0,5 of 50% recombinatie zoals wij verwachten voor twee merkers die onafhankelijk segregeren), dan verkrijgen we L(½). Dat is dan de probabiliteit dat we die waarneming doen als de twee merkers volledig onafhankelijk overgeërfd worden. Voor die waarneming binnen die familie is L(0,5) = 1/16. Dit betekent dat zelfs als de twee merkers volledig onafhankelijk zijn er 1 kans op 16 is dat er in een familie zoals hierboven beschreven slechts 1 recombinatie wordt waargenomen.Beide probabiliteiten (L(q) en L(½)) hebben een waarde tussen 0 en 1. Absoluut betekenen deze getallen echter niet veel omdat ze sterk afhangen van het aantal geobserveerde haplotypes in de familie.

Daarom definiëren we de lod score Z(q) als: Z(q)=log [ L(q)/L(0,5)]

Die formule geeft dan een absolute maat voor hoeveel waarschijnlijker het is dat wij een bepaalde waarneming doen in een familie (experiment) als de recombinatie fractie q zou zijn, dan als die 0,5 zou zijn.
Door q te laten variëren tussen 0 en 0,5 kunnen we de maximale lod score en de meest waarschijnlijke recombinatiefractie bepalen. Een maximale lod score >3 bij een recombinatiefractie q wordt als significante evidentie voor koppeling met de recombinatie fractie q beschouwd. Dit betekent dat een bepaalde waarneming in een familie duizend maal waarschijnlijker is bij koppeling van twee merkers met een recombinatiefractie q dan bij onafhankelijke segregatie van deze merkers. Een lod score van -2 wordt als significantiegrens voor niet-koppeling genomen.
In het voorbeeld hier is:

Z(q) = log[16(1-q)3q]
Dus voor
q = 0 is Z(q) = -∞
q = 0,05 is Z(q) = - 0,164
q = 0,1 is Z(q) = 0,067
q = 0,25 is Z(q) = 0,227
q = 0,35 is Z(q) = 0,187

De probabiliteit dat twee of meer onafhankelijke waarnemingen samen voorkomen is het product van de probabiliteiten voor elke waarneming afzonderlijk. Lod scores zijn logaritmes, lod scores voor twee markers bekomen in verschillende families kunnen dus opgeteld worden. Bekomen we zo een score > 3 dan zijn beide markers gekoppeld met een bepaalde maximale recombinatiefractie q. Bekomen we een score < -2 dan is koppeling bij die q uitgesloten. Merk op dat van het ogenblik dat er één recombinant haplotype wordt opgemerkt, de lod score bij q=0 noodzakelijk -∞ is of de probabiliteit voor q = 0 is 0.
In de praktijk zal men dus nieuwe waarnemingen blijven doen tot Z(q) groter is dan 3. Is Z(q) > 3 dan zegt men dat de twee merkers gekoppeld zijn en de q waarbij Z(q) maximaal is, geeft de afstand tussen de twee merkers. Is Z(q) < -2, dan zegt men dat de koppeling van de twee merkers met een deze q uitgesloten is.

Nog enkele nuttige definities:
Genetische kaart: een genetische kaart is een verzameling geordende, gekoppelde merkers die verspreid zijn over het volledige genoom. De afstand tussen de merkers wordt gemeten als % recombinatie en uitgedrukt in cM. De genetische kaart van de mens omvat ongeveer 3000 cM.
Genetische heterogeniteit: als er verschillende genen zijn die onafhankelijk van elkaar éénzelfde fenotype veroorzaken, dan spreken we van genetische heterogeniteit.
Penetrantie: soms leidt de aanwezigheid van een allel niet altijd tot het fenotype dat hiermee samenhangt. We spreken dan van onvolledige penetrantie. Als een individu het allel bezit, vertoont het het fenotype, of niet. Als we spreken van 80% penetrantie, betekent dit dat 80 % van de individuen die het allel bezitten ook het fenotype vertonen
Variabele expressie: de aanwezigheid van een allel bij verschillende individuen kan tot een verschillende ‘ernst’ van het fenotype leiden. Meestal is dit het gevolg van het effect van andere (modifier) genen.
Pleiotrope effecten – allelism: soms kunnen de verschillende allelen van een gen tot verschillende fenotypes leiden. Zo kan bijvoorbeeld een null allel tot een ernstig complex klinisch syndroom leiden en een missense puntmutatie in hetzelfde gen enkel tot mentale retardatie. Dit noemen we pleiotropisme of allelisme.