MUZE & REDE ; Grondbeginselen

MUZIKALE TEMPERAMENTEN

bij Westerse Muziekinstrumenten

April 2024 ; Ir. Johan Broekaert ; broekaert.devriendt@gmail.com (naar Inhoud)

	Inhoud
Woord vooraf	Kwart	Middentoon (kwart komma middentoon)
Klanken	Grote terts	1/5 Komma Middentoon
Sinusoïdale Klanken	Kleine terts	Silbermann (1/6 komma)
Het opwekken van sinusoïdale trillingen	Grote sext	Welgetemperd
De gespannen snaar	Tritonus	Werckmeister III
Toonhoogte van een snaar	Akkoorden ; meer dan twee noten	Kirnberger III
Monochord	Toonladders	Vallotti
De luchtkolom	Melodie en Harmonie	Neidhardt 1
Samengestelde Klanken	Noten	Bach en de Welgetemperde Middentoon
Harmonische Klanken	Toonhoogte van noten	Optimalisatie van een welgetemperd klavier
Grafische en Spectrale vergelijking	Pentatoniek	Minimalisatie van de onreinheden
Harmonische Afwijkingen	Diatonische toonladder	Minimalisatie van de spreiding van onreinheden
Twee- en driedimensionale trillichamen	Intervallen	Optimalisatie van een welgetemperd klavier op basis van interval verhouding
Geluidswaarneming door het oor	Eigenschappen	Evaluatie van Onreinheden
Geluidsniveau en -frequentie	Chromatische toonladder	Minimum spreiding eigenschappen
Samenklanken	Natuurlijk harmonische toonladder	Onreinheid van diatonische kwinten en grote en kleine tertsen
Zwevingen	Toonaarden	Belang van halftonen
Intervallen	Temperamenten	Tonaliteit
Prime	Berekening op basis van de frequentie van zwevingen	Een Zwevende Musicologie
Octaaf	Het Gelijkzwevend Temperament	Bibliografie
Kwint	De wolfskwint

Woord vooraf (terug naar Inhoud)

“Toegepaste Wetenschappen” : het precies stemmen van de piano van mijn echtgenote volgens het gelijkzwevend temperament, met behulp van een professionele laboratorium frequentie meter van zeer hoge precisie - meer dan acht cijfers precies -, heeft geleid tot een grote teleurstelling bij haar en mijn oudste dochter, … mijn echtgenote heeft in haar jeugd het geluk gehad om voor het stemmen van haar piano verwend te zijn geweest door J. Trappeniers (1902- ?), een toen in Brussel en Vlaanderen populair muzikant en componist, die als bijverdienste auditief piano’s stemde - zuiver op het oor dus -. Om zijn werk te beoordelen speelde hij na het stemmen steeds enkele muziekstukjes.
Overleg na dit gelijkzwevend piano stemmen, en ook het ophalen van de notenleer uit haar jeugd, bracht bij mijn echtgenote de vaststelling naar boven, dat één octaaf een totaal van 53 komma’s omvat, ...- drie en vijftig komma’s ! ! -, … vanwaar in ‘s hemels’ naam die drie en vijftig komma’s ?

Met drie en vijftig komma’s in één octaaf is het dus niet mogelijk dat de twaalf halve tonen van één octaaf zouden gelijk zijn. Het begin van een lange doch leerrijke en aangename zoektocht, gepaard aan het vier jaar lang slijten van een broek op de banken van de muziekacademie van Mortsel, waar men het in Keulen hoorde donderen, ...

Deze tekst is niets meer dan een grotendeels vulgariserende doch strikt rationele beschrijving van elementen en structuren in de muziek, waarmee een componist, een dirigent, een muzikant, artistieke talenten kan ontplooien en voorbrengen tot meerder luistergenot van toehoorders en publiek. Meer diepgaande lectuur is natuurlijk mogelijk, bijvoorbeeld bij Kelletat H. (1981, 1982), Rasch R. (1984), Jedrzejewski F. (2002), Sethares W. (2005), Di Veroli C. (2008), Calvet A. (2020), , enz … Fundamenteel gesproken is er niets nieuws onder de zon, en zijn de meeste elementen die in deze tekst worden besproken reeds gekend van sinds het begin van de 18-de eeuw, … en soms zelfs veel vroeger, en toch blijven veel vragen dikwijls onbeantwoord, zelfs al bestaat het antwoord reeds lang.
Deze tekst is vergelijkbaar met de wetenschappelijke beschrijving van de kleuren, vormen en perspectief van schilderijen, of van de structuur en scheikundige samenstelling van eetwaren, drank of geuren ; deze dragen eveneens niets bij tot de artistieke waarde van een doek, of tot de prestaties van kok, œnoloog, parfumeur, … maar laten toe de zaken beter te begrijpen en waarderen.

De mooie muziekkunst op zich, vanaf inspiratie over het componeren tot het uitvoeren, wordt in deze tekst niet besproken.

De tekst omvat het resultaat van talloze en langdurige individuele opzoekingen, analyses en bevindingen betreffende muzikale temperamenten. Hij zou niet mogelijk geweest zijn, zonder moderne opzoekmogelijkheden en rekenmiddelen. Helaas blijft recente wetenschappelijk literatuur soms toch nog steeds moeilijk bereikbaar, zelfs als is ze dikwijls tot stand gekomen dank zij financiering door de overheid, - door de bevolking dus -.
De tekst betreft het muzikaal stemmen van westerse muziekinstrumenten met vaste toonhoogtes, klavieren in het bijzonder, zoals bijvoorbeeld orgels, piano’s, klavecimbels, maar ook blaas- en snaarinstrumenten, en dergelijke meer.
Hij heeft tot doel een zo breed mogelijke muzikale en rationele verklaring te omvatten, van de elementen die bepalend zijn voor het stemmen van een instrument, kortom, voor het bekomen van een gewenst temperament.

Temperamenten kwamen historisch tot stand, soms intuïtief, ingevolge de auditieve waarneming van samenklanken, - intervallen en akkoorden -, op basis van een fijn, gevormd en ontwikkeld muzikaal oor en gevoel, dikwijls zelfs zonder een hieraan gepaarde musicologische analyse.
    Op basis van de verzamelde bevindingen, kan men vaststellen dat haast alle historisch voorgestelde temperamenten neerkomen op een streven naar verbetering van de grote tertsen binnen de diatonische toonladder op C-groot, met als gevolg dat de betrokken kwinten binnen deze toonladder iets verminderen op het gebied van hun toonhoogte-verhouding.
    Voor temperamenten waarvoor een analyse werd uitgewerkt en gepubliceerd, kan men bemerken dat de meeste analyses werden uitgevoerd op basis van afwijkingen van de verhoudingen van toonhoogtes of op basis van proportionele verdeling van komma's, dikwijls ook uitgedrukt in cents in plaats van verhoudingen, wat mogelijke berekeningen sterk vereenvoudigt en versnelt.
    Achteraf bekeken kan men een mogelijk en tamelijk éénzijdig gehecht belang aan komma's, verhoudingen of cents verrassend vinden, gezien de totstandkoming van temperamenten op basis van auditieve waarnemingen vooral gebaseerd was op zeer fijnzinnige waarneming van zwevingen binnen samenklanken. Aldus bekeken, kampt de musicologie met een zwaar onderschat historisch probleem, waarbij men onvoldoende bewust gewerkt heeft met twee maten en twee gewichten : de auditieve maat van de muzikant en stemmer, en de meetkundige maat met verhoudingen, van de musicoloog, dit laatste vooral ingevolge Pythagoras. Het gevolg is dat er heel wat temperamenten zijn waarvoor men niet met zekerheid weet wat primeert in de beoordeling ; er is een probleem van wat eerst komt, de kip of het ei, - of anders gezegd, de zwevingen of de verhoudingen ? -.Dit werk werkt daarom verdere en enigszins vernieuwende analyses uit op het gebied van structuur van historische temperamenten en minimalisatie van zwevingen.

Om volledig en goed onderbouwd te zijn, bevat de tekst soms uitgewerkte en narekenbare natuurkundige en mathematische benaderingen. Deze berekeningen mogen bij een lezing gerust overgeslagen worden : begrip van deze analyses is niet vereist om de tekst zinvol en verstaanbaar te kunnen lezen ; voor een vlotte en goede lezing volstaat het om de juistheid van de berekeningen te geloven en te aanvaarden.

Ondanks alle in dit werkje soms verregaand besproken rationele elementen , blijft het zó, dat muziek een kunst is, een kunst door het oor en voor het oor, op een bedje van menselijke emoties en artistieke vrijheid.

KLANKEN (Terug naar Inhoud)

Muziek is een geordende vorm van geluid, en omvat meestal een ritmische opeenvolging van gestructureerde en in de tijd gespreide klanken.

Leopold II, (1835-1909) ; Belgische koning : “Muziek is een geluid dat veel kost” [ ¹ ]

Een waarneembaar geluid komt tot stand door trillingen in de lucht, die zich in de omgeving voortplanten met een snelheid van circa 340 meter per seconde ; dit is de snelheid van het geluid.

Muzikale klanken komen tot stand door het trillen van fysieke elementen, waarbij deze elementen contact hebben met de lucht, al dan niet via een klankbord, om aldus hun trillingen aan de lucht over te dragen.
Fysieke elementen kunnen meerdere dimensies of vormen hebben. Zo heeft men elementen met één dimensie, bijvoorbeeld een snaar of de luchtkolom van een blaasinstrument. Men kan ook twee dimensies hebben, bijvoorbeeld een gespannen vel op een pauk of trommel. Drie dimensies komen ook voor, zoals onder anderen de resonatoren van H. von Helmholtz (1821-1894) die werden gebruikt voor onderzoek naar de structuur van klanken, maar zeker gekend zijn de klokken. Uiteindelijk kan men ook zeer complexe trillende lichamen hebben, de menselijke zangstem is hiervan het voorbeeld bij uitstek.

Alle hierboven vermelde klanken kunnen van elkaar verschillen, zelfs al hebben zij eenzelfde toonhoogte ; zij hebben een bepaald “timbre” of klankkleur. Een specifieke klankkleur volgt uit een welbepaalde samenstelling van de klank, die een specifieke som bevat van afzonderlijke sinusoïdale klanken.
Een klank kan verschillen volgens de kracht waarmee hij wordt opgewekt ; meestal heeft men meer componenten van hogere frequentie wanneer de klank met meer kracht wordt opwekt. Uitstervende klanken veranderen in de tijd ook van samenstelling ; meestal sterven componenten met hogere frequentie, sneller uit.

Tegenwoordig kunnen klanken ook elektronisch worden verwekt, anders dan met fysieke elementen. Instrumenten die dit mogelijk maken worden synthesizers genoemd. Bij synthesizers worden de elektronische trillingen overgebracht aan de lucht bij middel van een elektrisch aangestuurd membraan, - een luidspreker -. Synthesizers laten toe om klanken samen te stellen die niet, of maar zeer moeilijk, kunnen voortgebracht worden door fysiek trillende elementen.

SINUSOÏDALE KLANKEN (Terug naar Inhoud)

Een sinusoïdale trilling is de meest elementaire natuurlijke vorm van trillen ; hij is de basisvorm van trillingen, waarmee alle andere klanken in de natuur kunnen worden samengesteld. Een sinusoïdale trilling kan mathematisch voorgesteld worden door :

Een sinusoïdale trilling kan ook grafisch voorgesteld worden, en dit geeft een beeld van de wijze waarop een deeltje in de tijd over en weer beweegt

Waarbij :
- A : de amplitude van de trilling
- f : de frequentie van de trilling
- T : de periode van de trilling
- ϕ : de fase van de trilling (het ogenblik waarop de trilling begint)
- t : de tijd

Meestal komen sinusoïdale trillingen in de natuur voor als gedempte trillingen. Een demping is het gevolg van interne wrijvingen van het trillend lichaam en/of van wrijvingen met zijn omgeving, zelfs al is deze dikwijls niet meer dan wat lucht. Een gedempte sinus kan worden weergegeven als :

Waarbij < σ > de dempingsfactor is, die bepaalt hoe snel de amplitude afneemt in de tijd. Zie ook de figuur hieronder

HET OPWEKKEN VAN SINUSOÏDALE TRILLINGEN (Terug naar Inhoud)

"Men moet altijd weten waarom ..." (Paul Valéry 1871-1945 [ ² ] ), "... en hoe" (mijn moeder)

Twee fysieke elementen bij uitstek, naast andere mogelijkheden, kunnen leiden tot het opwekken van een zuivere sinusoïdale trilling, of een strak gestructureerde som ervan, deze zijn : een gespannen snaar, of een luchtkolom in een luchtpijp.

GESPANNEN SNAAR (Terug naar Inhoud)

Uit de figuur hieronder kan men de evenwichtstoestand bepalen van een elementair deeltje van een snaar, dat buiten zijn begintoestand werd gebracht.

Element van een gespannen snaar

Het infinitesimaal snaarsegment AB met < m > als massa per lengte eenheid, en met een lengte < dx > heeft een massa < mdx >.
Een infinitesimale kracht < dF₁ > op dit snaarsegment, ingevolge haar versnelling of vertraging is dus (kracht = massa maal versnelling) :

Anderzijds moet deze infinitesimale kracht ook gelijk zijn aan het infinitesimaal verschil < dF₂ > van de krachten < F_A > en < F_B >. Dit verschil is evenredig met de lengte < dx > van het infinitesimaal segment AB en met het verschil in helling tussen A en B. Een verschil in helling van een curve is gelijk aan de tweede afgeleide van de curve, - de lijn van de aangeslagen en dus gekromde gespannen snaar -. Men kan aldus stellen :

Gelijkstelling van beide infinitesimale krachten dF₁ en dF₂ leidt tot :

Dit stelt een lopende golf voor, met snelheid , en heeft als algemene oplossing :

Specifiek, voor een tussen twee punten gespannen snaar met lengte < l₀ >, heeft men als mogelijke oplossing :

Bovenstaande formule voor de trilling van een snaar werd reeds door B. Taylor [1715, p. 113-118] uitgewerkt, en stelt een staande sinusgolf voor.

TOONHOOGTE geproduceerd door een snaar (Terug naar Inhoud)

Eigenschappen van de bekomen oplossing. Voor n = 1 bekomt men :

een golflengte :

een toonhoogte : Frequentie

Elke gehele waarde van n groter dan één, leidt tot een golflengte die een factor < 1/n > kleiner is, en een frequentie die een factor < n > hoger ligt. Men heeft dus een reeks van mogelijke oplossingen, die een onderling harmonisch verband hebben, wat betreft de muziek.

De uiterste knopen van deze staande golven liggen natuurlijk in de ophangpunten van de snaar.

MONOCHORD (Terug naar Inhoud)

Bij een vaste en gegeven trekkracht op een snaar, ‑ bij een gegeven spanning dus ‑, en volgens de formule hierboven, is de frequentie van de bekomen toon, omgekeerd evenredig met de lengte van de snaar. Ingevolge dit omgekeerd evenredig verband is het mogelijk om op basis van lengteverhoudingen de verhouding tussen toonhoogtes te bepalen. Dit kan bij middel van een monochord.

Het monochord is een meettoestel, volgens de principe tekening hieronder, met één snaar onder constante spanning dank zij een gegeven gewicht, waardoor een gewenst omgekeerd evenredig verband tussen lengte en frequentie verzekerd wordt. De lengte van het trillend gedeelte < AB > van de snaar kan worden ingesteld bij middel van een verschuifbare brug, op positie in onderstaande tekening. Pythagoras heeft zeer waarschijnlijk met het monochord gewerkt.

Men kan voor alle posities Bn van deze monochord stellen :

f₁.AB₁ = f₂.AB₂ = … = f_n.AB_n = constant

DE VIOOL “Koningin Elisabethwedstrijd”

De viool zal vermoedelijk wel zowat het belangrijkste snaarinstrument zijn.

Eugène Ysaÿe, viool leraar van koningin Elisabeth (1876-1965), zou in antwoord op een delicate vraag, van haar ooit gezegd hebben : “Elle joue comme une reine”, ‑ “Ze speelt als een koninging” ‑ ?

LUCHTKOLOM (Terug naar Inhoud)

De figuur hieronder toont een infinitesimaal luchtschijfje in een luchtkolom vóór en na een kort tijdstip gelijk aan < dt >.

Element van een luchtkolom

Ingevolge de inertie van het luchtschijfje, ondergaat dit naast de drukkracht < S.dp > de volgende versnellingskracht :

zodat

Ingevolge de druk in de buis en de algemene gaswet waarbij PV = constant, kan men stellen :

waaruit

Na differentiatie naar < x > bekomt men

Het gelijk stellen van de twee formules voor δp/δx geeft :

De bovenstaande formule werd reeds uitgewerkt door Rayleigh (1877, p. 188 - 191). Deze gelijkheid staat opnieuw voor een golfvergelijking, en voor een eindige buis kan men dezelfde oplossing vooropstellen, gelijk aan deze bij een snaar met een staande golf. Bij een eindige buis kan men op het uiteinde van de buis zowel een knoop als een buik hebben, al naar gelang de buis afgesloten of open is. Bij een half open buis heeft men zowel een buik als een knoop, en de grootst mogelijke golflengte is dan gelijk aan vier maal de lengte van de buis.
Ingevolge de algemene gaswet, geldt de bovenstaande vergelijking ook voor de druk, de gasdichtheid en zelfs de temperatuur. Men kan dus ook spreken van een druk-, dichtheids- en temperatuurgolf.

SAMENGESTELDE KLANKEN. (Terug naar Inhoud)

Elke trilling, - elke klank ; timbre ; klankkleur -, kan samengesteld worden uit een som van sinusoïdale trillingen.
Deze samenstelling kan zeer geordend zijn, bijvoorbeeld doordat de frequenties van de verschillende sinussen een geheel veelvoud zijn van elkaar, maar kan ook tot in een uiterste mate ongeordend zijn, ingevolge een willekeurige samenstelling van amplitudes, frequenties en fases.
Een door ieder gekende extreme vorm van ongeordende klank is ruis ; deze omvat een zeer brede reeks van talloze sinusoïdale componenten. Men spreekt van witte ruis, indien gans het hoorbaar spectrum continu sinusoïdale componenten omvat, met een gelijke amplitude voor alle componenten. Men kan een zeer goede benadering van witte ruis horen bij een niet goed afgestemde analoge FM-radio- of TV-ontvanger ; bij digitale telecommunicatie is er ook ruis, maar deze is ingevolge de digitale modulatie- en demodulatietechnieken niet meer waarneembaar.

HARMONISCHE KLANKEN. (Terug naar Inhoud)

“… voor een nauwkeurigere behandeling van de harmonie is het belangrijk om elk interval te kennen naar zijn ware naam en in zijn eigenlijke verhouding…” [Kirnberger 1771, p. 21].

Per definitie is een harmonische klank, een klank opgebouwd uit een reeks van sinussen die allen een frequentie hebben die nagenoeg gelijk is aan een geheel veelvoud van een basisfrequentie, zoals men bijvoorbeeld heeft bij de klank van een snaar of een blaasinstrument, - een luchtkolom -.
De sinus met basisfrequentie f₁ krijgt de naam “grondharmonische” of ook grondtoon, en de volgende sinussen met frequentie f_n, gelijk aan n x f₁, met < n > een geheel getal, worden de “n-de harmonische” of ook boventonen genoemd.
Mathematisch kan dit voorgesteld worden als :

of ook

Élke periodieke klank < F(t) > is samengesteld uit harmonischen. Dit werd mathematisch aangetoond door J. Fourier (1768-1830). De sinusoïdale componenten van een klank kunnen uit de golfvorm berekend worden door toepassing van een Fourier analyse, bij middel van :

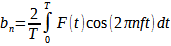
Indien de periodiciteit van F(t) niet gekend is, dan kunnen de bovenstaande integralen in functie van de gewenste precisie uitgewerkt worden over een voldoend grote tijd, - een voldoend groot aantal periodes -.

GRAFISCHE EN SPECTRALE VERGELIJKING (Terug naar Inhoud)

Er bestaat een enorme diversiteit aan klanken, met specifieke klankkleur of timbre ; dit correspondeert dus met een grote diversiteit aan mogelijke golfvormen. Bij wijze van voorbeeld wordt hieronder de golfvorm van een lage noot van een piano voorgesteld (B0; Bruckner buffetpiano) en van een kerkorgel (de lage langgerekte D1, uit de Toccata en Fuga in D-klein, BWV 565 van J.S. Bach).

Golfvorm van de laagste “Si” van een Bruckner buffetpiano

Golfvorm van de laagste “Re” van een kerkorgel

Beide klanken verschillen sterk, ook visueel qua golfvorm. Bij het orgel is de periodiciteit visueel gemakkelijker waarneembaar.
Het verschil valt ook duidelijk op, bij de beschouwing van de spectrale samenstelling, bekomen door berekening van de Fourier integralen over meer dan 50 perioden

Frequentiespectrum van de laagste “Si” van een Bruckner buffetpiano

Frequentiespectrum van de laagste “Re” van een kerkorgel

De spectrale analyses tonen duidelijk de rijkdom van de klanken aan : men kan tot meer dan 30 harmonischen waarnemen,
Analyse van de frequenties van harmonischen toont aan dat de hogere harmonischen van de piano steeds verder naar boven afwijken van de theoretisch verwachte waarde. Bij het orgel daarentegen blijft men redelijk nauw bij de theoretische waarden aansluiten ; bovendien nemen ze minder snel in amplitude af. Op basis van de criteria frequentie en amplitude blijkt het orgel een beter gevulde en reinere klank (-kleur) te hebben.

HARMONISCHE AFWIJKINGEN (Terug naar Inhoud)

Indien de frequenties van de harmonischen afwijken van een geheel veelvoud van de frequentie van de grondtoon, dan worden deze componenten van het spectrum eerder benoemd als “partiëlen”, en niet meer als “harmonischen”.
Afwijkingen van de theoretische harmonische indeling voor de hogere partiëlen, leidt bij het auditief stemmen van een piano bij voorbeeld, tot afwijkingen van de theoretische waarde van de grondharmonische van een klank. De oorzaak waarom de snaren afwijken van het ideaal theoretisch model, is dat het ideaal mathematisch berekend model beantwoordt aan : perfecte ophangpunten en homogeniteit, en een gebrek aan stijfheid en interne wrijving van de snaren. De hogere partielen liggen gewoonlijk hoger dan verwacht. Opdat enkele dominante harmonischen die sterker zijn dan de grondharmonische beter zouden samenvallen moeten de grondharmonischen noodzakelijk iets lager liggen. Een beter mathematisch model van een snaar is mogelijk op basis van een differentiaal vergelijking van de vierde orde, die leidt tot onderstaande formule (Fletcher H., 1962, vol. 34, p. 749-761).

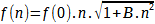met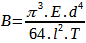

waarbij E = elasticiteitsmmodulus (Young) en T = spanning

Deze afwijkingen in frequentie van de grondharmonischen werden ooit opgemeten door O. L. Railsback [1938], zie de gepubliceerde grafiek hieronder.
De verticale schaal geeft de afwijkingen op in cents. Deze logaritmische eenheid wordt veelvuldig gebruikt in de muziek, bij metingen van afwijkingen in toonhoogte. Omwille van de logaritmische eigenschap zijn de verhoudingen van toonhoogtes gemakkelijk te bepalen, want men kan gemakkelijke optellingen maken, in plaats van ingewikkelde vermenigvuldigingen, delingen en het trekken van complexe wortels.

Uitrekking van octaven bij een auditief gestemde piano

Één cent komt overeen met de logaritme van het honderdste deel van een halve toon - vanwaar de naam -, wat overeenkomt met het 1.200-ste deel van een octaaf. Mathematisch uitgedrukt :
1 cent komt overeen met de verhouding

Gelijkaardige doch ongebruikelijke alternatieve eenheden zijn :

de < Savart > [(10)^(1/1000)=1.00230524…], en de < mil > [2^(1/1000)=1.00069339...].

TWEE- en DRIEDIMENSIONALE TRILLICHAMEN (Terug naar Inhoud)

Een mathematische analyse van de spectra van deze trillichamen, toont aan dat hun spectrum sterk kan afwijken van het eenvoudig model dat werd vastgesteld bij snaren en luchtpijpen, waar de harmonischen een frequentie hebben dat in principe gelijk is aan een geheel veelvoud van de frequentie van de grondharmonische.
Ook hier gebruikt men bij voorkeur de term “partiëlen”, wat betreft de hogere sinusoïdale componenten van de klank.

GELUIDSWAARNEMING DOOR HET OOR (Terug naar Inhoud)

Geluid, muziek, treedt het binnenoor binnen via een gehoorgang (2) en bereik aldus het trommelvlies (4). Vandaar loopt het over hamer (6), aambeeld (7) en stijgbeugel (8), tot bij het ovaal venster (5) aan de ingang van het slakkenhuis (10).

Het geluid loopt verder door de opgerolde buis van het slakkenhuis, dat met vloeistof is gevuld en een basilair membraan bevat dat de buis over zijn lengte in twee deelt. Beide delen staan met elkaar in verbinding op het einde van de buis, en het tweede deel eindigt in een rond venster, terug vooraan in deze buis. De ontrolde lengte van het slakkenhuis bedraagt ongeveer 35 mm.
    Op het basilair membraan staan ongeveer 25.000 "buitenste trilhaartjes" die het ontvangen geluid versterken, en ongeveer 3.500 "binnenste trilhaartjes". De binnenste trilhaartjes prikkelen de gehoorzenuw, die de signalen doorgeeft aan de hersenen.
    Het basilair membraan is stijf en smal aan de ingang bij het ovaal venster en wordt elastischer en breder naar de top van het slakkenhuis.     Het trilt mee met het ontvangen geluid ; de hoogste frequenties aan de zijde van het ovaal venster, de laagste aan de top.
    De plaats waar het meetrillen met het inkomend geluid maximaal is, is dus functie van de frequentie, en ligt van hoog naar laag over de lengterichting van het basilair membraan verdeeld. Het oor realiseert aldus een bepaalde frequentie analyse, enigszins vergelijkbaar met de analyse via een Fourier integraal. Onderstaande figuur illustreert ruwweg deze frequentieverdeling over dit membraan [Van de Heyning P., 2019].

Basilair membraan : approximatieve verdeling van frequenties

Het oor is gevoelig voor frequenties tussen 20 tot 20.000 Hertz, en kan zeer fijne frequentieverschillen opmerken binnen dit bereik. Toonhoogte verschillen van 0,5 % zijn waarneembaar voor muzikaal getrainde waarnemers (Britannica), d. i. dus voor f₁/f₂~ 1,005…, of ook ~ 8 cents.
De wijze waarop een muzikaal getraind persoon toonhoogteverschillen zo fijn kan herkennen zonder gebruik van meetapparatuur, is nog niet volop begrepen. De frequentie selectiviteit van het basilair membraan en van de trilhaartjes zou niet volstaan om de selectiviteit van het oor in zijn geheel te verklaren zoals hierboven verondersteld. De hersenen, "het muzikaal geheugen", en wellicht ook andere elementen zoals bijvoorbeeld de klankkleur, het geluidsniveau en dergelijke meer, spelen mogelijk ook een belangrijke rol.

GELUIDSNIVEAU en -FREQUENTIE (Terug naar Inhoud)

Meetbare karakteristieken van het oor op gebied van geluidsniveau en -frequentie blijken niet lineair te verlopen ; beiden verlopen eerder quasi logaritmisch.
De werking van het oor is nog steeds het onderwerp van diepgaand en zeer complex onderzoek. Het oor kan bijvoorbeeld ook zélf geluid produceren [Kemp D. 1978]. Bij waarneming van twee verschillende tonen bijvoorbeeld, kunnen er ingevolge de niet-lineariteit ook fictieve tonen gehoord worden met een frequentie gelijk aan het verschil van de frequenties (Tartini, 1754, p. 13 [ ³ ]), misschien ook de som :

“Gegeven twee klanken van welk muziekinstrument dan ook, die kunnen worden uitgebreid en de klank zo lang als gewenst wordt versterkt (trompetten, jachthoorns, strijkinstrumenten, hobo, enz.), hebben we een derde klank ; geproduceerd door de botsing van twee luchtvolumes die door de twee gegeven geluiden worden verplaatst.
De manier waarop dit derde geluid wordt geproduceerd, doet er voor de huidige fysieke behoefte niet toe; het feit is genoeg, en dit moet worden uitgelegd.”

Het oor heeft een zeer hoog dynamisch bereik: de verhouding in geluidssterkte tussen de onderste gehoorgrens en het bovenste pijnniveau ligt hoger dan een factor 1/100.000. De gevoeligheid is ook afhankelijk van de frequentie, binnen een band die ligt tussen ongeveer 20 en 20.000 Hertz. Bij het ouder worden vermindert de gevoeligheid van het oor door verzwakking van de buitenste haarcellen. De buitenste haarcellen kunnen ook beschadigd geraken en definitief hun functie verliezen bij blootstelling aan te hoge geluidsintensiteit, wat leidt tot gehoorschade of verzwakking van het gehoor.

De onderliggende figuur geeft een ruwe schets van de gevoeligheid van het oor bij een normaal volwassen persoon.
De "foon" lijnen zijn lijnen van gelijke gevoeligheid, en deze lijnen werden experimenteel bepaald door proeven met een representatieve groep luisteraars. In de figuur zijn foon-lijnen van gelijke luidheid uitgetekend, in functie van de frequentie, ten overstaan van het overeenkomend objectief meetbaar geluidsniveau gemeten in decibel. De figuur toont dat het oor het gevoeligst is rond een frequentie van ongeveer 3.000 Hz, en dat deze gevoeligheid snel vermindert naar hogere frequenties, en vooral ook naar lagere frequenties toe.

Het menselijk oor : foon-lijnen met gelijke gevoeligheid

Bij de frequentie 1.000 Hz wordt de "foon" gelijk gesteld aan de "decibel". Het geluidsniveau in decibel is een objectieve maat voor de door het geluid veroorzaakte drukvariaties. Het geluidsniveau in decibel wordt bekomen door toepassing van de formule hieronder, waarin p₀ een genormaliseerde referentie drukvariatie is en p₁ de gemeten drukvariatie veroorzaakt door het geluid. De waarde van p₀ in de lucht is genormaliseerd op 20 microPascal (20 μP) ; ISO 389-5.

Vb: - De geluidsdruk (-variatie) bij 80 dB is 10.000 maal sterker dan de geluidsdruk bij 0 dB.
- Een geluidsdruk verhouding gelijk aan 2, komt overeen met ongeveer 6 dB verschil

Noot : 1 Pascal = 1 Newton/m²
1 Newton = de kracht op 1 kg massa, versneld aan 1 m/s²

SAMENKLANKEN (Terug naar Inhoud)

ZWEVINGEN (Terug naar Inhoud)

Het tegelijk afspelen van verschillende klanken, ook van verschillende toonhoogte, - verschillende noten dus -, is een normale en courante praktijk in de muziek ; het is een belangrijk integrerend deel ervan. Hierbij wordt er meestal gestreefd naar een reinheid van de bekomen samenklank : men wenst een goede harmonie, consonantie, mooie akkoorden dus, en dissonantie is gewoonlijk ongewenst, tenzij die bedoeld is voor het bekomen van bepaalde affecten.
Een reine samenklank, - goede consonantie -, vereist dat waarneembare zwevingen tussen klanken niet storend zouden zijn. Een objectieve maat van welke zwevingen storend zouden zijn, is een complex onderwerp, dat nog steeds bestudeerd wordt, en waar een eerste mijlpaal werd gesteld door R. Plomp en W. J. M. Levelt [1965]. Zij maakten duidelijk dat in functie van de betrokken grondtonen er een onaangenaam gevoel is vanaf een zekere relatief lage zwevingsfrequentie, om bij hogere zwevingsfrequenties terug te verdwijnen, waarbij de grondtonen opnieuw klinken als twee afzonderlijke klanken, of als één “reine” klank. Voor de eenvoud bij berekeningen, zal er voor de zwevingen verondersteld worden dat ze voldoende laag moeten zijn in frequentie, en indien zo, dat bij vergelijking van zwevingen, ze zo klein of zo gelijk mogelijk in frequentie zouden zijn.
Zwevingen ontstaan door interferentie tussen de partiëlen, - sinussen dus -, met nagenoeg gelijke frequentie, van de onderscheiden klanken. Twee sinussen van nagenoeg gelijke frequentie, kunnen in het oor klinken als één sinus die in amplitude is gemoduleerd, en dit kan bij bepaalde modulatiefrequenties storend zijn, - dissonant dus -. De som van twee willekeurige sinussen kan mathematisch uitgewerkt worden :

Deze som van sinussen kan dus gezien worden als één sinus, gekenmerkt door :

een gemiddelde frequentie (f_a+ f_b)/2
een amplitude modulatie van (a-b) tot (a+b), bij een frequentie gelijk aan (fa – fb)
en een fase modulatie van geringe invloed gelijk aan

De figuur hieronder illustreert het effect :

INTERVALLEN (Terug naar Inhoud)

Bij het tegelijk spelen van verschillende noten, mogelijk ook met verschillende klank, zijn er toonafstanden die een voorkeur genieten, doordat ze voor deze bepaalde toonafstanden een groot aantal partiëlen hebben met gelijke frequentie.
Deze toonafstanden zijn muzikaal gesproken < rein >. De belangrijkste reine toonafstanden worden hieronder besproken. Deze specifieke toonafstanden hebben elk een naam, die functie is van het aantal noten dat kan geteld worden tussen de onderste en de bovenste toon. Deze naamgeving wordt later duidelijk, bij het bespreken van toonladders.

PRIME (Terug naar Inhoud)

De afstand tussen twee tonen met éénzelfde frequentie, heeft in de muziek de naam < prime >. De prime heeft dus een verhouding < 1/1 > tussen grondtonen.
Zelfs al zijn er mogelijk verschillen in amplitude, demping en fase, toch zullen de harmonischen van beide klanken steeds samenvallen en dus versmelten tot één nieuwe klank.
Bij afwezigheid van zwevingen spreekt men van een perfect unisono. Zodra er echter een klein verschil in frequentie optreedt kunnen harmonischen van de ene klank zweven met nabij liggende harmonischen van de andere klank. Dit verschijnsel is bijna steeds overduidelijk waarneembaar. Voor een prime bedraagt de zwevingsfrequentie tussen de grondtonen f₁ en f₂ :

Noot : bij negatief verschil heeft men het over “onderzweving” ; bij positief verschil heeft men het over “bovenzweving”.

OCTAAF (Terug naar Inhoud)

Het octaaf is de eerstvolgende toonverhouding dat een grote samenval van harmonischen omvat, en heeft een verhouding 2/1.
De frequentiespectra van beide klanken zijn hieronder samen weergegeven. Voor de eenvoud van de tekening en van de uiteenzetting wordt verondersteld dat alle getekende harmonischen éénzelfde amplitude hebben.

Alle even harmonischen van f₁ vallen samen met alle harmonischen van f₂ : 67% van alle harmonischen vallen dus samen. Ingevolge deze zeer sterke consonantie, krijgen de noten die een octaaf verschillen dezelfde naam, indien nodig mits toevoeging van indices die verwijzen naar het getroffen octaaf.
De laagst waarneembare zweving heeft plaats tussen de 2-de harmonische van f₁ en de grondtoon van f₂. De frequentie van deze zweving bedraagt :

KWINT (Terug naar Inhoud)

De kwint heeft een verhouding 3/2 tussen grondtonen (f₂/f₁= 3/2). De frequentiespectra van de klanken staan geschetst in de figuur hieronder.

Alle derde harmonischen van f₁ vallen samen met alle even harmonischen van f₂ : 40% van alle harmonischen vallen dus samen.
De laagst waarneembare zweving heeft plaats tussen de 3-de harmonische van f₁ en de 2-de harmonische van f₂. De frequentie van deze zweving bedraagt:

KWART (Terug naar Inhoud)

De kwart heeft een verhouding 4/3 tussen grondtonen (f₂/f₁= 4/3). De frequentiespectra van de klanken staan geschetst in de figuur hieronder.

Alle vierde harmonischen van f₁ vallen samen met alle derde harmonischen van f₂ : 29% van alle harmonischen vallen dus samen.
De laagst waarneembare zweving heeft plaats tussen de 4-de harmonische van f₁ en de 3-de harmonische van f₂. De frequentie van deze zweving bedraagt:

GROTE TERTS (Terug naar Inhoud)

De grote terts heeft een verhouding 5/4 tussen grondtonen (f₂/f₁= 5/4). De frequentiespectra van de klanken staan geschetst in de figuur hieronder.

Alle vijfde harmonischen van f₁ vallen samen met alle vierde harmonischen van f₂ : 22% van alle harmonischen vallen dus samen.
De laagst waarneembare zweving heeft plaats tussen de 5-de harmonische van f₁ en de 4-de harmonische van f₂. De frequentie van deze zweving bedraagt:

KLEINE TERTS (Terug naar Inhoud)

De kleine terts heeft een verhouding 6/5 tussen grondtonen (f₂/f₁= 6/5). De frequentiespectra van de klanken staan geschetst in de figuur hieronder.

Alle zesde harmonischen van f₁ vallen samen met alle vijfde harmonischen van f₂ : 19% van alle harmonischen vallen dus samen.
De laagst waarneembare zweving heeft plaats tussen de 6-de harmonische van f₁ en de 5-de harmonische van f₂. De frequentie van deze zweving bedraagt:

GROTE SEXT (Terug naar Inhoud)

De grote sext heeft een verhouding 5/3 tussen grondtonen (f₂/f₁= 5/3). De frequentiespectra van de klanken staan geschetst in de figuur hieronder.

Alle vijfde harmonischen van f₁ vallen samen met alle derde harmonischen van f₂ : 25% van alle harmonischen vallen dus samen.
De laagst waarneembare zweving heeft plaats tussen de 5-de harmonische van f₁ en de 3-de harmonische van f₂. De frequentie van deze zweving bedraagt:

TRITONUS (Terug naar Inhoud)

In de klassieke notenleer, wordt de tritonus gezien als een dissonant interval. Dit interval wordt aldus genoemd, omdat het drie gehele tonen omvat.
Men kan onder bepaalde voorwaarden een tritonus hebben die toch consonant is, - bijna rein -. Een "reine” tritonus heeft een toonverhouding 7/5 tussen grondtonen (f₂/f₁= 7/5). Bij afwijking hiervan heeft men de hieronder opgegeven zweving :

AKKOORDEN ; of meer dan twee noten (Terug naar Inhoud)

Een zeer klassieke combinatie omvat bijvoorbeeld het samenbrengen van vier klanken met frequentieverhoudingen 1, 5/4, 3/2 en 2/1, maar er zijn nog talloze andere mogelijkheden.
Bij de hier gestelde combinatie is het alsof er een nieuwe klank ontstaat met grondfrequentie gelijk aan f₁/4, maar waarvan een aantal harmonischen ontbreken: zoals de grondtoon zelf, en de harmonischen met rang 2, 3, 7, 9, 11, 13, 14, 17, 19, 21, 22, 23 ….
Zie de figuur hieronder: alle bestaande harmonischen vallen steeds samen met een verdeling of tussenverdelingen op f₁, representatief voor de harmonischen op f₁/4.

Het is meestal niet eenvoudig of evident om de samenklank van muzikale akkoorden rationeel te verduidelijken en te verklaren, zoals gedaan in dit voorbeeld.
Het is zelfs mogelijk dat bepaalde klanken mooi samenklinken op bepaalde muziekinstrumenten, en op andere dan weer niet, afhankelijk van de harmonische structuur van de klank van het instrument.
De klassieke muziekleer bestudeert zeer grondig de harmonie van akkoorden, en de "Harmonieleer" is voor klassieke muziek een uitzonderlijk belangrijk vak.

TOONLADDERS (Terug naar Inhoud)

MELODIE EN HARMONIE (Terug naar Inhoud)

Melodie betreft klanken die mooi op elkaar volgen.
Harmonie betreft klanken die mooi samen klinken.
Het < mooi > zijn betekent meestal dat er geen of slechts onbeduidende zwevingen zijn, zoals bij de hierboven beschreven intervallen werd besproken. Op basis van een mooie samenklank, zowel melodisch als harmonisch, werden toonladders uitgewerkt.

NOTEN (Terug naar Inhoud)

Het is mogelijk om bij middel van de besproken intervallen standaard reeksen van klanken op te bouwen. Een dergelijke reeks wordt een “toonladder” genoemd ; de individuele klanken in een dergelijke reeks worden dan “noten” genoemd. Een eerste mogelijke reeks betreft een opeenvolging van octaven, zowel naar boven als naar onder. Alle aldus bekomen noten krijgen eenzelfde naam, maar het aantal aldus bekomen noten is echter onvoldoende voor de muziek. Bruikbare toonladders omvatten daarom ook kwinten, maar ook met behulp van andere intervallen kunnen toonladders gebouwd worden. De noten krijgen dan verschillende namen.
In de westerse muziek heeft men zeven noten.
De moderne naamgeving van noten komt van G. Arezzo (991-1033) op basis van de reeks ut, re, mi, fa, sol, la, uit het lied :

Ut queant laxis
Resonare fibris
Mira gestorum
Famuli tuorum
Solve polluti
Labii reatum,
Sancte Iohannes

Mogen uw dienaren
met zachte stem
uw wonderdaden
doen klinken ;
Verlos onze bezoedelde lippen van schuld,
heilige Johannes.

Sterk ondersteunend voor de diatonische toonladder is het kinderliedje “Broeder Jacob”, oorspronkelijke in het Frans “Frère Jacques”, dat ook in andere talen populair is (zie internet, met trefwooorden “broeder” en “Jacob”).

Broeder Jacob, slaapt jij nog ?
Do re mi do, mi fa sol
Hoort de klokken luiden, bim, bam, bom.
Sol la sol fa mi do, do sol do.

Recent ook heeft men het Do-Re-Mi lied uit de film “The Sound of Music” (1965).

Doe: a deer, a female deer (do)
Ray: a drop of golden sun(re)
Me: a name I call myself (mi)
Far: a long, long way to run )fa)
Sew: a needle pulling thread (sol)
La: a note to follow so (la)
Tea: a drink with jam and bread (si, ti)

Later werd de si als zevende noot toegevoegd (i.p.v. Sa). De si wordt soms vervangen door ti, om geen twee noten te hebben die met een letter < S > beginnen. De ut werd vervangen door do, op grond van gemakkelijker klankvorming. Eerste sporen van naamverandering van ut naar do zijn terug te vinden in geschriften van G.M. Bononcini [17-de eeuw].
De naam van een noot in een tekst kan voluit geschreven zijn, of vermeld bij middel van een symbool, meestal een letter. De naamgeving bij middel van een symbool kan verschillen volgens de taal of het land. In deze tekst wordt meestal de naamgeving gebruikt, die in de Angelsaksische landen of internationaal het meest gebruikelijk is, en waaraan indien zinvol, een octaafnummer kan worden toegevoegd.

do	re	mi	fa	sol	la	si
C	D	E	F	G	A	B

Voor gewijzigde noten kan er in geschreven teksten aan de noot een symbool < # > (kruis) worden achtergevoegd voor een verhoging, of (mol) voor een verlaging. Er bestaat een belangrijk verschil met het Duits taalgebied, waar de letter staat voor de < verlaagde si > , en de letter < h > voor de “natuurlijke” noot < si >. Soms wordt binnen geschreven teksten het achtervoegsel < is > bij de letter toegevoegd, voor een verhoging, en < es > voor een verlaging.

TOONHOOGTES (Terug naar Inhoud)

Toonhoogtes worden gemeten in Hertz, afgekort Hz., waarbij één Hz. overeenkomt met één trilling per seconde.

Dat een toon een trillingsverschijnsel van de lucht is, met een wel te bepalen objectief meetbare frequentie, werd aangetoond door R. Hooke (1635-1703), door het produceren van een toon bij middel van een gekarteld wiel, ‑ een wiel met insnijdingen aan de rand ‑, dat aan een meetbare en dus gekende snelheid wordt gedraaid. Pas veel later herhaalde F. Savart (1791-1841) een zelfde experiment, bij middel van wat gekend is als “het wiel van Savart”. Het meten van toonhoogtes is dus pas redelijk recent mogelijk geworden.

De toonhoogte van de noot < C > wordt historisch geassocieerd met de toon die voortgebracht wordt door een orgelpijp met een lengte van één voet. Hierdoor kan deze toonhoogte van streek tot streek verschillen, wegens verschillen in lengtes van de voet, of van maten in het algemeen. Bovendien verandert de toonhoogte met de temperatuur en de druk van de lucht. De toonhoogte van de C noot zou vandaag ongeveer 281 Hz zijn, op basis van de moderne gestandaardiseerde duim (één duim = 25,4 mm). De aan deze C noot gepaarde A noot, zou op basis van een reine, normale < C‑A > interval-verhouding (5/3 ; een grote sext) ongeveer gelijk zijn aan 469 Hz.
 De toonhoogte van de < la > noot, < A > dus, is tegenwoordig standaard vastgelegd op de waarde 440 Hz [Londen, 1939, 1955 ; ISO 16, 1975].
 De noot A, op 440 Hz, ligt bij een moderne piano in het vierde octaaf. Indien het rangnummer van de laagste A op een piano gelijk aan nul wordt verondersteld, dan wordt de A op 440 Hz benoemd als A4 . Alle andere noten van C tot B binnen het A4 octaaf krijgen dan op dezelfde wijze een rangnummer 4 . In Frankrijk worden de octaven één eenheid lager geteld ; men kan dus stellen : A4 (internationaal) = La3 (Frankrijk).
 Er zijn ooit meerdere andere toonhoogtes als stemvork gangbaar geweest, ook op andere noten, zoals hierboven besproken bijvoorbeeld de noot < C >. De mogelijke toonhoogtes lagen ooit redelijk ver uiteen, van hoog rond 480 Hz (chorton, Duitse barok), tot laag rond 392 Hz (Franse barok), en 415 Hz wordt nog altijd redelijk frequent gebruikt door clavecinisten of voor barokmuziek.

PENTATONIEK (Terug naar Inhoud)

Men kan een reeks opeenvolgende kwinten bouwen, waarbij men de toonhoogte dus steeds met een factor 3/2 verhoogt of verlaagt. Men kan de reeks beperken tot 5 noten, waarbij men dan de collectie noten uitbreidt door op deze noten octaven te bouwen.
Men kan veel variante reeksen opbouwen. Onderstaande tabel geeft een mogelijke reeks, teruggebracht tot één octaaf, en dat goed aansluit bij de moderne westerse toonladders :

Noot	C	D	F	G	A
Verhouding	1	3²/ 2³	2² / 3	3 / 2	3³ / 2⁴
Verhouding	1	1,125	1,333...	1,5	1,6875
Toonhoogte	260,74	293,33	347,65	391,11	440,00

Merk de stijgende machten van 3 op, in de volgorde F(-1), C(0), G(1), D(2), A(3), het is alsof de volledige reeks F-C-G-D-A vanuit F naar boven toe is opgebouwd.

DIATONISCHE TOONLADDER (Pythagoras, ca. 582 v.C. – 500 v.C) (Terug naar Inhoud)

De pentatonische toonladder kan naar boven toe verder uitgebreid worden tot zeven noten. Men bekomt de verhoudingen volgens de tabel hieronder.

Noot	C	D	E	F	G	A	B	C
Verhouding	1	3²/ 2³	3⁴/ 2⁶	2²/ 3	3 / 2	3³ / 2⁴	3³ / 2⁷	2
Toonhoogte	260,74	293,33	330,00	347,65	391,11	440,00	463,54	521,48
Interval	Prime	Seconde	Terts	Kwart	Kwint	Sext	Septiem	Octaaf

Ook hier verandert de macht van 3 steeds met een stap gelijk aan < één >, bij een lezing in de volgorde F-C-G-D-A-E-B. Deze volgorde heeft een muzikaal belang, bij het bepalen van de tonaliteit van een muziekstuk ; dit wordt verder nog verduidelijkt. De toegevoegde noten laten ook toe een alternatieve pentatonische toonladder op te bouwen : C-D-E-G-A.

INTERVALLEN (Terug naar Inhoud)

In bovenstaande tabel staan een aantal intervallen onder hun naam opgegeven. Zoals reeds besproken, kunnen intervallen rein zijn, maar binnen deze toonladder zijn alleen maar de kwinten en kwarten rein.
    Een interval kan worden benoemd op basis van een rangnummer ten overstaan van de onderste noot ; als voorbeeld in deze tabel is de C-noot de onderste noot voor alle opgegeven intervallen, maar een interval kan ook gebouwd en dus benoemd worden ten overstaan van eender welke noot.
    Nieuw binnen deze tabel, zijn de seconde en de septiem. Op te merken valt dat er per interval verschillende toonhoogte verhoudingen mogelijk zijn.
    Zo heeft men voor de terts twee verschillende waarden : de grote terts C-E bijvoorbeeld, met een verhouding 81/64 (i.p.v. 5/4 ; = 1,265), en de kleine terts E-G, met een verhouding 32/27 (i.p.v. 6/5 ; 1,185). De tertsen zijn hier bovendien dus ook niet rein.
    Het verschil binnen deze toonladder, tussen de grote terts en de reine grote terts wordt de “syntonische komma” genoemd, en de verhouding ervan bedraagt (81/64) / (5/4) = 81/80 = 1,0125.
    Zo heeft men ook voor de seconde twee verschillende waarden : een verhouding 9/8 voor C-D, D-E, F-G, G-A en A-B, en een verhouding 2⁸/3⁵ (1,0535…) voor E-F en B-C.

Een interval kan ook benoemd worden in functie van zijn grootte, dit is, in functie van de toonhoogte verhouding tussen een bovenste en een onderste noot. Men heeft aldus een hele toon, bijvoorbeeld tussen de bovenvermelde C-D, D-E, F-G, G-A, A-B en een halve toon tussen E-F en B-C. De termen < hele toon > en < halve toon > dekken approximatieve waarden van toonhoogte verhoudingen, deze termen mogen niet mathematisch exact worden geïnterpreteerd.

DIATONISCHE EIGENSCHAPPEN (Terug naar Inhoud)

Een diatonische toonladder heeft als specifieke eigenschap opgebouwd te zijn met een opeenvolging van twee hele tonen, gevolgd door een halve toon, verder gevolgd door drie hele tonen, om af te sluiten met een halve toon.

De hierboven vermelde reeks opeenvolgende noten < C-D-E-F-G-A-B-C > is effectief diatonisch. In de tabel hierboven spreekt men van de “diatonische toonladder in C-groot”, omdat hij begint met een grote terts C-E op de beginnoot C.

Men kan de bovenstaande reeks noten ook lezen en verder zetten vanaf de noot A, met behoud van de hierboven tussen noten vastgestelde toonafstanden. Men bekomt aldus de reeks < A-B-C-D-E-F-G-A>. Gelezen vanaf de noot A, hebben we dus een verschillende volgorde van hele en halve tonen. Ook deze reeks is van belang in de muziek, men noemt ze de “diatonische toonladder in A-klein” omdat ze op de beginnoot A een kleine terts A-C heeft.

CHROMATISCHE TOONLADDER (Terug naar Inhoud)

Verdere uitbreiding met kwinten naar boven toe, leidt tot de noten F#, C#, G#, en naar onder toe tot de noten Bb, Eb, Ab De bekomen verhoudingen zijn gemakkelijk na te rekenen.

Noot	Bb	Eb	Ab	G#	C#	F#
Verhouding	2⁴ / 3²	2⁵/ 3³	2⁷/ 3⁴	3⁸/ 2¹²	3⁷/ 2¹¹	3⁶/ 2⁹
Toonhoogtes	463,54	309,03	412,03	417,66	278,44	371,25
Decimaal	0,777...	1,185...	1,580...	1,601...	1,067...	1,898...

De noten G# en Ab hebben nagenoeg dezelfde verhouding, ; het verschil in hun verhoudingen wordt de “pythagoreïsche komma” genoemd en bedraagt 3¹²/2¹⁹ = 1,01364… . Noten die nagenoeg dezelfde toonhoogte hebben, zodanig dat ze muzikaal eventueel omwisselbaar zijn, zijn “enharmonisch” : in deze tabel zijn Ab en G# enharmonisch.
    Het verschil tussen de pythagoreïsche komma en de syntonische komma, wordt op zijn beurt als “schismatische komma” benoemd, en bedraagt 5.3⁸/2¹⁵ = 1,00113… De syntonische komma is in de muziektheorie belangrijker dan de pythagoreïsche : de reine en de pythagoreïsche grote terts die een syntonische komma verschillen kunnen beide samen voorkomen in een toonladder, terwijl twaalf opeenvolgende reine kwinten vereist zijn om een pythagoreïsche komma te kunnen ervaren, en dit komt alleen voor in klavierinstrumenten die over het geheel pythagoreïsch gestemd zijn, wat haast niet meer voorkomt, maar wel met orgels het geval geweest is tot in de middeleeuwen.
    Deze toonladder heeft twee soorten halve tonen : natuurlijke halve tonen, die noten met een verschillende naam omvatten, zoals bijvoorbeeld C#-D, D-Eb, E-F, enz…, en de chromatische halve tonen, zoals C-C#, Eb-E, enz…, die gelijknamige noten omvatten,
    De natuurlijke halve tonen hebben een toonhoogteverhouding 2⁸/3⁵ = 1,0535 , dicht bij de verhouding van 4 opeenvolgende pythagoreïsche komma’s.

(1,01364…)⁴ = 1,05570… ≈ 1,0535

De chromatische halve tonen hebben een toonhoogteverhouding 3⁷/2¹¹ = 1,06787 , dicht bij de verhouding van 5 opeenvolgende pythagoreïsche komma’s.

(1,01364…)⁵ = 1,07010… ≈ 1,06787

Een hele toon komt bijgevolg overeen met ongeveer negen komma’s. In zijn geheel heeft deze toonladder 53 komma’s. Deze chromatische toonladder, met de hier gedefinieerde 53 komma's voor hele en halve tonen, vormt de basis van de "klassieke" notenleer.

Met deze chromatische toonladder wordt het mogelijk om allerhande nieuwe pentatonische toonladders te gebruiken, een op piano gemakkelijk te spelen alternatief is de toonladder F#-G#-Bb-C#-Eb door alleen maar de “zwarte”toetsen te spelen. Verder kan men ook op andere noten dan C of A, een diatonische toonladder bouwen. Deze varianten worden dan genoemd naar de eerste noot van de ladder ; bijvoorbeeld de “diatonische toonladder in < D-groot >, die reeks noten < D-E-F#-G-A-B-C# > omvat ; dit kan ook op enige andere noot ; let op de ongewijzigde volgorde van hele en halve tonen, indien gelezen vanaf de noot D.

Het klein verschil tussen G# en Ab heeft er toe geleid, dat men zich de noten kan voorstellen in de volgorde waarin ze zijn ontstaan, alsof ze een sluitende cirkel vormen waarbij G# bij Ab aansluit, om van daar uit opnieuw dezelfde reeks af te lopen : de kwintencirkel. Deze cirkel bevat aldus twaalf noten, zoals ook een klassiek muziekklavier twaalf toetsen per octaaf heeft, waarbij de octaven aan elkaar aansluiten.

Op de kwintencirkel kan men bij middel van koorden ook de tertsen aanduiden en hij wordt dikwijls gebruikt om besproken muzikale karakteristieken beeldmatig voor te stellen, door deze te merken of te illustreren op de bogen van de kwinten, of de koorden van de tertsen.

Kwintencirkel

Men kan de chromatische toonladder ook verder uitbreiden naar boven en onder toe, met dubbele kruisen < ## >, en dubbele mol < bb >. Men kan de noten dan bijvoorbeeld voorstellen op een kwintenspiraal, waarop er door lichte verschuivingen mogelijk ook rekening kan worden gehouden met de pythagoreïsche komma. Let in de figuur ook op de ligging van enharmonische noten ; bovenaan bijvoorbeeld de noten , A, Bbb, G##.

Kwinten-”spiraal”

In principe zou men steeds verder kunnen gaan tot meerdere wijzigingstekens. Er kan nagerekend worden dat men opnieuw een quasi sluitende cirkel bekomt voor 24 noten (met een komma = 3²⁴/2³⁸=1,0275…), en veel beter nog voor 53 noten (met een zeer kleine komma =3⁵³/2⁸⁴=1,00209...). Er volgen nog veel stappen waarbij men een goede sluiting van de cirkel bekomt, maar de eerstvolgende stap die nóg beter is dan 53 opeenvolgende kwinten, ligt bij zo maar eventjes 306 opeenvolgende kwinten (met een komma =3³⁰⁶/2⁴⁸⁵=0,99898…, omgekeerd is dit ook =1,00102… ; dit komt overeen met 1,8 cent) ; dit overstijgt het onderscheidend vermogen van het muzikaal geschoold menselijk oor.
In de praktijk worden twee of meer wijzigingstekens op één noot zelden of nooit gebruik. Dit belet niet dat er klassieke westerse muziek wordt gecomponeerd met andere of méér noten dan deze die hier zijn opgegeven. Men heeft muziek met kwartnoten, een andere tonale indeling, en zelfs ook microtonale muziek.

NATUURLIJK HARMONISCHE TOONLADDER (Terug naar Inhoud)

Buiten de kwint en haar omgekeerde, de kwart, zijn ook andere reine intervallen belangrijk, voornamelijk de tertsen. De natuurlijk harmonische toonladder wordt opgebouwd bij middel van reine kwinten, kwarten, en reine grote en kleine tertsen.
De belangrijkste bronnen betreffende deze toonladder, gaan terug tot Aristoxenos, 4-de eeuw v.C., Ptolemaeus, 90-168 n.C., en Zarlino, 1517 – 1590.
Men kan de reine kwinten en grote en kleine tertsen overzichtelijk en systematisch in een schema voorstellen, zoals in de figuur hieronder.

Natuurlijk harmonische toonladder : “Tonnetz”-structuur
    Kwinten : zie horizontale pijlen
    Grote tertsen : zie vertikale pijlen
    Kleine tertsen : zie schuine pijlen

Deze toonladder heeft een zeer strakke structuur, opgebouwd met < onvervormbare > driehoeken, net zoals driehoeken met vaste zijden ook in de geometrie strak onvervormbaar zijn.
De bovenstaande figuur is geïnspireerd op het < Tonnetz > concept voor toonladders, volgens figuur hieronder [Euler 1739, p. 147].

Euler : Tonnetz

Een uitbreiding naar dubbele wijzigingstekens is desgewenst mogelijk. Het kan bijvoorbeeld ook zo getekend en opgevat worden, dat de noten cyclisch herhaald worden op een toroïde [D. Gerhard, H. Hu, 2019, fig. 10].

Toroïde met natuurlijk harmonische structuur

Naast al de hierboven geïllustreerde reine intervallen, bevat de diatonische toonladder op C twee opvallende intervallen ; een kwint < D-A > en kleine terts < D-F > die niet rein zijn. Deze wijken een syntonische komma af van het rein interval. Dit heeft als gevolg dat de intonatie tijdens de uitvoering van een muziekstuk lichtjes in toonhoogte kan stijgen of dalen, indien deze intervallen voorkomen in een melodie, waarbij deze intervallen tóch rein worden gespeeld.

C	2 / 1	De nevenstaande tabel overloopt de toonverhoudingen, van onder tot boven gerangschikt van laag naar hoog Bij vergelijk van de waarden in deze tabel met deze van de pythagoreïsche toonladder stelt men vast : Men heeft meer reine intervallen, en veel verhoudingen zijn redelijk eenvoudig, wat bijdraagt tot een betere welluidendheid Bij enharmonische noten zijn de kruisen kleiner dan de mollen in plaats van groter. Anders gezegd : de natuurlijke halve tonen zijn groter dan de chromatische halve tonen, in plaats van het omgekeerde, zoals bij de pythagoreïsche chromatische toonladder. Men heeft aldus vijf komma’s voor de natuurlijke halve tonen, en vier voor de chromatische ; in totaal dus 55 komma’s binnen één octaaf, in plaats van 53, zoals in de klassieke notenleer wordt gesteld. Een gepaste waarde van de halftonen is zeer belangrijk voor de klassieke zang. De kleinere chromatische halftonen binnen deze toonladder hebben een sterke uitdrukkingskracht, en het belang hiervan wordt zeer uitgebreid en sterk benadrukt en besproken door Kelletat [1994].
B	15 / 8
Bb	16 / 9
A#	225 / 128
A	5 / 3
Ab	8 / 5
G#	25 / 16
G	3 / 2
Gb	74 / 45
F#	45 / 32
F	4 / 3
E	5 / 4
E b	6 / 5
D#	75 / 64
D	9 / 8
Db	16 / 15
C#	25 / 24
C	1

TOONAARDEN (Terug naar Inhoud)

De gewijzigde noten, uitgewerkt zoals hierboven, of in lijn met Pythagoras door opeenvolgende vermenigvuldigingen of delingen door 3/2, zijn muzikaal van belang. Ook de gewijzigde noten moeten op een notenbalk kunnen genoteerd worden, voor uitvoering in de muziekpraktijk.

Indien de wijziging op een noot slechts sporadisch voorkomt, dan wordt het wijzigingsteken #, of b op de notenbalk rechtstreeks vóór de noot genoteerd. Aldus genoteerde wijzigingen blijven alleen geldig in de maat waarin ze genoteerd staan, en dit over alle gelijke en volgende noten van die maat.
"Gewijzigde" noten worden op dezelfde lijn als de oorspronkelijke noten genoteerd, maar om permanente wijzigingen duidelijk te maken en niet bij elke noot te moeten herhalen, kunnen de wijzigingstekens vooraan op de notenbalk worden genoteerd. De aldus genoteerde voortekens zijn bepalend voor de toonaard van een muziekstuk. Indien in een notenbalk met voortekens toch terug een ongewijzigde noot gewenst wordt, dan wordt dit aangeduid met een herstelteken < herstel >. De volgorde waarin de kruisen of mollen ontstaan volgens opeenvolgende kwinten, is ook de volgorde waarbinnen ze afhankelijk van de toonaard als wijzigingsteken op een notenbalk worden aangebracht, volgens de figuren hieronder.

De reeds aangehaalde natuurlijke diatonische toonladder in C-groot, zoals voorgestgeld bij de pythagoreïsche en natuurlijk harmonische toonladder, bevat alleen maar ongewijzigde < natuurlijke > noten. Er kan worden nagegaan dat al deze noten bij elkaar aansluiten op een halve cirkelboog van de kwintencirkel (zie figuur). Andere toonaarden liggen ook in een halve cirkelboog op deze cirkel, maar weliswaar op de cirkel over een hoek verschoven. Hoe meer kwinten men verschuift, hoe meer voortekens men krijgt.

Veranderingen van toonaard tijdens de uitvoering van een muziekstuk komen veel voor ; men spreekt dan over het moduleren, en deze techniek kan allerhande affecten ondersteunen. De toegevoegde gewijzigde noten zijn daarom even belangrijk als de oorspronkelijke zeven. Hieronder een overzicht van toonaarden, en de overeenkomende voortekens.

Geen - of -	C (*)	a (*)
#	G (*)	e (*)	b	F(*)	d (*)
##	D (*)	b (*)	bb	Bb (*)	g (*)
###	A (*)	f# (*)	bbb	Eb (*)	c (*)
####	E (*)	c# (*)	bbbb	Ab (*)	f (*)
#####	B (*)	g# (*)	bbbbb	Db (*)	bb (*)
######	F# (*)	d# (*)	bbbbbb	Gb (*)	eb (*)
#######	C# (*)	a#	bbbbbbb	Cb (*)	ab (*)

Hoofdletters : grote terts toonaarden
kleine letters : kleine terts toonaarden
(*): Alle toonaarden gemerkt met (*) , werden gebruikt in "Das Wohltemperierte Klavier" van J. S. Bach.

Men kan muziek hebben, die niet steunt op de structuur van een diatonische toonladder, en die alle twaalf noten gelijk behandelt. Men heeft bijvoorbeeld atonale muziek, dodecafonie, en ook microtonale muziek, niet-westerse muziek, enz…

TEMPERAMENTEN (Terug naar Inhoud)

De tot nog toe besproken toonladders bevatten allemaal onreine intervallen, die een rem zijn voor kwalitatieve en brede modulaties van toonaarden. Dit heeft geleid tot het temperen van intervallen, waarbij onreinheden over meerdere intervallen gespreid worden en dus minder opvallen, of zelfs acceptabel worden.
    Tijdens de late-barok is de belangstelling voor de toepassing van reine tertsen sterk gegroeid, gepaard aan een zoektocht naar globale en optimale reinheid binnen een diatonische toonladder, voornamelijk deze op C-groot. Er werden toen talloze toonladders voorgesteld, -temperamenten dus-. Men kan de pythagoreïsche en de harmonische toonladders zien als hun voorlopers of prototypes.
    In beschikbare historische beschrijvingen van temperamenten, worden toonverhoudingen dikwijls precies beschreven, meestal in breuken, later ook in cents, maar de wijze waarop het beschreven temperament werd bekomen wordt dikwijls niet vermeld. Mogelijk gebeurde de verdeling van de onreinheden dikwijls auditief.
    Het goed stemmen van een instrument gebeurt in principe op het oor : het is het oor dat auditief oordeelt of een samenklank aanvaardbaar is of niet. De aldus auditief bekomen temperamenten kunnen na het stemmen worden geanalyseerd, zodat men er karakteristieke eigenschappen kan aan toekennen, opdat ze zouden kunnen beschreven en gerepliceerd worden. Historisch gezien steunen het overgrote deel van de analyses op het bepalen van toonverhoudingen of op het verdelen ervan, steunend op berekeningen en nametingen op een meetinstrument. Het historisch meest besproken meetinstrument daartoe, betreft de monochord, maar de precisie van dit instrument is beperkt omwille van de precisie van de harmonische structuur van een snaar. Nameting hiervan toont aan dat een tweede of derde harmonische van een snaar reeds tot een factor 1,004 kan afwijken van de theoretische waarde ; zie ook Raes G.-W. [ ^]4 ]. Het is dus niet altijd zeker of de gepubliceerde waarden de werkelijke verhoudingen precies weergeven (zie ook : Harmonische Afwijkingen).
    Om bovenstaande redenen, zal de theoretische uitwerking van historische temperamenten verder in deze tekst altijd gebeuren op basis van zwevingsfrequenties, een alternatieve wijze waarop er rechtstreeks en met meer preciesie kan aangesloten worden bij mogelijke rechtstreekse waarnemingen met het oor. Maar zelfs aldus, kunnen de berekeningen nog steeds niet op een exacte wijze de auditieve waarnemingen bevestigen, gezien de complexe werking van het oor en de inharmoniciteit van de trillende lichamen, … de harde en werkelijke aard van reële fysisch acoustische fenomenen, die onmogelijk in volledig juiste mathematische modellen kunnen gegoten woren. Deze alternatieve berekeningen zijn gelukkig en waarschjnlijk meestal wel voldoende om een aantal gevolgtrekkingen te kunnen voorbrengen.

BEREKENINGEN OP BASIS VAN DE FREQUENTIE VAN DE ZWEVINGEN. (Terug naar Inhoud)

“Wiskunde zwemt bekoorlijk onder het muzikaal oppervlak” E. E. Helm (1928- [ ⁵ ]

Er bestaan talloze temperamenten. Daarom worden de herberekeningen met gelijke verdeling van de komma door gelijke verdeling van de frequenties van de zwevingen, hier beperkt tot een zeer beperkt aantal temperamenten die geschiedkundig bij de belangrijkste horen.
Het is gebruikelijk om auditief te stemmen, op alle noten die binnen de F3-F4 partitie liggen [Calvet A., 2020]. Het gebruik van deze partitie heeft deels historische gronden, en ze omvat de langste niet omwikkelde snaren van een piano, zodat ze op dit instrument een rijke en beste harmonische structuur hebben. Bij dit stemmen wordt gezocht naar een optimalisatie van alle kwinten, kwarten en grote en kleine tertsen die binnen dit bereik deel uitmaken van de diatonische toonladder op C-groot. Om de toonhoogtes te berekenen kunnen onderstaande formules worden toegepast, alhoewel er moet op gewezen worden dat ze de zwevingen maar zeer rudimentair berekenen, voor lage initiële zwevingsfrequenties, want ze houden geen rekening met het consonantievenster volgens Plomp en Levelt (1965), en ook niet met de inharmoniciteit van snaren of geluid in het algemeen :

q_F=2C4-3F3	q_C=4G3-3C4	q_G=2D4-3G3	q_D=4A3-3D4
q_A=2E4-3A3	q_E = 4Bb3-3E4	q_B=4F#3-3Bb	q_F_#=2C#4-3F#3
q_C_#=4G#3-3C#4	q_G_#=2Bb-3G#3	q_Eb=4Bb3-3Eb4	q_Bb=4F3-3Bb3

Kwinten en kwarten binnen F3-E4

p_F=4A3-5F3

p_C=4E4-5C4

p_G=4B3-5G3

Grote tertsen binnen F3-E4

r_D=10F3-6D4

r_A=5C4-6A3

r_E=10G3-6E4

r_B=5D4-6B3

Kleine tertsen binnen F3-E4

HET GELIJKZWEVEND TEMPERAMENT of ook : evenredig zwevend (Terug naar Inhoud)

WOLFSKWINT (Terug naar Inhoud)

De kwint op < G# > of < Ab > is zeer onrein, in het geval van een Pythagoreïsch systeem beperkt tot twaalf noten, dat drie < # >. en drie bevat, zoals reeds getekend op de kwintencirkel. Deze kwint wordt om die reden ook wel “wolfskwint” genoemd.
De sterke onreinheid van de kwint op < G # > of < Ab > kan voor een eerste en meest “eenvoudige” verbetering bijvoorbeeld worden weggewerkt door een gelijke verdeling van zijn onreinheid over alle kwinten. Hierdoor bekomt men een perfecte sluiting van de kwintencirkel, met een enharmonie van de noten < G # > en < Ab > , maar ook bij alle andere gewijzigde noten, zoals bijvoorbeeld < A# > en < Bb >, enz ...

In de klassieke muziektheorie is het gelijkzwevend temperament niet écht gelijkzwevend, maar heeft men over alle noten een gelijke verhouding voor gelijke intervallen. Het wordt daarom soms ook het Evenredig Zwevend Temperament genoemd, omdat de frequentie van een zweving evenredig is met de frequentie van de grondnoot van het interval.

Het was niet eenvoudig om mathematisch of meetkundig twaalf verkleinde kwinten te bepalen, met een gelijke toonverhouding die leidt tot een gesloten kwintencirkel. Deze verdeling moet gekend zijn, wil men ze kunnen instellen of nameten, bijvoorbeeld op een monochord. Daartoe moet men dus een twaalfde wortel van twee kunnen bepalen. In principe kan dit door twee maal een vierkantswortel te trekken, gevolgd door een derde macht wortel.
Rekenkundige bepaling : exacte rekenkundige bepaling van een derde macht wortel zou gekend zijn sinds Aryabhata (476 n.C.), een Indisch astronoom.
Meetkundige bepaling. Een vierkantswortel kan gemakkelijk bepaald worden door toepassing van de stelling van Pythagoras op een rechte driehoek, volgens Euclides (ca. 300 v.C.). Zie figuren hieronder.

Een derde macht wortel kan bepaald worden bij middel van een constructie volgens Nicomedes (ca. 280 v.C. - ca. 210 v.C.), zie Verbeken B. [2016, p. 21].

Constructie van Nicomedes

Noot :
De constructie van de driehoek ABC, vereist dat < k > kleiner moet zijn dan < 8 > en positief. Indien k > 8, dan wordt de basis van de driehoek groter dan de som van de twee opstaande gelijke zijden, en dit kan dus niet. Bij een groter getal deelt men het getal eerst door een derde macht van een geheel getal, tot wanneer men een grootste uitkomst heeft die tussen 1 en 8 ligt.
Verder is de wortel uit een negatief getal gelijk aan de negatieve waarde van de wortel uit het gelijk positief getal.

∆ BCD en ∆ AED zijn gelijkvormig :

∆ AEP en ∆ CQP zijn gelijkvormig :

zodat

Volgens Pythagoras voldoet AM binnen ∆ ABM en ∆ AQM aan :

zodat

hieruit of ook

zodat of

Vroege besprekingen van het gelijkzwevend temperament zijn afkomstig van Galilei [1581], Praetorius (1571-1621), Mersenne (1588-1648), en vroege mathematische uitwerkingen zijn gekend van Chu Tsai-Yu (1584) en S. Stevin [1585]. Ook Zarlino (1588) bespreekt dit temperament.

De onderstaande figuur uit het boek van Zarlino illustreert hoe men bij middel van opeenvolgende driehoeken een meetkundige reeks van verhoudingen kan tot stand brengen. De verhouding in hoogte tussende kleinste en de grootste driehoek is gelijk van twee, en dus heeft men een reeks die met de twaalfde wortel van twee toeneemt. De eerste stap moet daartoe wel gelijk zijn aan de twaalfde wortel van twee, en deze kan meetkundig bepaald worden door opeenvolgende wortels (zie hierboven), of eventueel ook door een benadering in opeenvolgende stappen, tot wanneer de tekening juist uitkomt (trial and error ; vallen en opstaan).

Zarlino : gelijke indeling van een octaaf

Stevin berekende gehele getallen waarmee de toonhoogtes evenredig zijn en die in stappen met een factor 2^(1/12) van elkaar verschillen ; 12 stappen tussen 5.000 voor de grondtoon, tot 10.000 voor het octaaf. De berekening is zeer merkwaardig, maar zijn reken methode heeft geleid tot enkele zeer lichte fouten ; zie de tabel hieronder.

Noot	C	C#	D	Eb	E	F
Stevin	5.000	5.296	5.611	5.944	6.298	6.674
Exact	5.000	5.297	5.612	5.946	6.300	6.674

Noot	F#	G	G#	A	Bb	B
Stevin	7.071	7.491	7.936	8.409	8.908	9.438
Exact	7.071	7.492	7.937	8.409	8.909	9.439

Stevin : gelijke verdeling van het octaaf

Ook merkwaardig is de benadering door B. Fritz [1757], die volgens zijn beschrijving geen gelijke verhoudingen nastreeft, maar inderdaad een gelijke en zeer kleine, doch niet nader gedefinieerde onreinheid van kwinten wenst.
Een werkelijke gelijkheid van de frequentie van zwevingen is alleen maar mogelijk binnen één octaaf ; per octaaf heeft men per definitie een verdubbeling van frequenties. Een berekend resultaat zal dus afhangen van de noot waarop het octaaf is gebouwd, en aldus zijn er 12 mogelijke oplossingen, één per gekozen grondnoot. Deze oplossingen verschillen echter quasi niet, qua absolute toonhoogte van de noten.
Voor het stemmen binnen een toonladder op de noot < F3 >, kunnen de toonhoogtes berekend worden op basis van de hierboven gegeven vergelijkingen, met als toegevoegde voorwaarden :

q = q_F = q_C = q_G = q_D = q_A = q_E = q_B = q_F# = q_C# = q_G# = q_Eb = q_Bb

en A3 = 220

Zie de onderstaande tabel, voor een vergelijking van de “klassieke waarden”, met deze bekomen voor gelijke zweving binnen het bereik F3-E4.

Noot	F3	F#3	G3	G#3	A3	Bb3
Klassiek	174,61	185,00	196,00	207,65	220,00	233,08
Zweving	174,66	185,05	196,00	207,69	220,00	233,15
q	- 0,80	- 0,80	- 0,80	- 0,80	- 0,80	- 0,80
p / r ; m	6,69		8,02		- 12,02

B3	C4	C#4	D4	Eb4	E4	F4
246,94	261,63	277,18	293,66	311,13	329,63	349,23
247,00	261,60	277,18	293,60	311,13	329,60	349,33
- 0,80	- 0,80	- 0,80	- 0,80	- 0,80	- 0,80	- 1,59
- 14,02	10,43		- 14,96		- 17,63	m = 96

Het gelijkzwevend temperament

De lijn in deze tabel geeft de zwevingsfrequenties op voor de grote tertsen op F, C, G ; de kleine tertsen op D, A, E, B ; en onderaan in de kolom F4, een voorgestelde instelling voor een metronoom die de instelling van de zwevingsfrequentie objectief kan ondersteunen.
De tertsen binnen het gelijkzwevend temperament zijn van mindere kwaliteit, omwille van hun betrekkelijk hoge zwevingsfrequenties.
Op de overgang van < E4 > naar < F4 >, verdubbelt de zwevingsfrequentie < q > van de kwinten. Anderzijds zijn de verschillen in toonhoogte met de “klassieke” waarden verwaarloosbaar : 0,32 cent gemiddeld, en 0,52 cent maximum. Ze zijn niet meetbaar met een monochord, en zijn zelfs met een moderne elektronische toonhoogtemeter zeer moeilijk vast te stellen. Het sluiten van de kwintencirkel bij het stemmen op het oor is moeilijk, omwille van de lage zwevingsfrequenties van alle kwinten en de afwezigheid van reine intervallen die als controle op het stemmen zouden kunnen dienen.

DE MIDDENTOON (kwart komma middentoon) (Terug naar Inhoud)

De middentoon resulteert uit een groeiend belang voor reine grote tertsen, tijdens de late Barok. Een klassieke toonladder kan hoogstens acht reine grote tertsen inhouden, want één grote terts omvat vier kwinten, en bij de middentoon wordt dit inderdaad aldus uitgewerkt. Deze wijze van stemmen werd door P. Aaron [1523] beschreven. Typerend is de daartoe vereiste gelijke vermindering van de kwinten die de reine grote terts C-E vormen, met 1/4 van een syntonische komma ; deze vorm van middentoon wordt daarom de 1/4-de komma middentoon genoemd ; ook genaamd als kwart komma middentoon.
De chronologie betreffende een aantal alternatieven kan revelerend zijn. De middentoon startte met de 1/4-de komma versie (Aaron 1523), later kwam de 1/5-de komma versie (Rossi 1666, Sauveur 1701), en nog later de 1/6-de komma versie (Romieu 1758). Een mogelijke hypothese is dat deze niet werden gecreëerd op basis van gemeten en berekende syntonische komma verdelingen, maar mogelijk wel zuiver auditief, zoals hieronder wordt uiteengezet ; zie : Di Veroli (2018), Fogliano (1529).

Een kwint die een kwart van een syntonische komma is verminderd, kan eventueel als volgt worden bekomen.
        Stem een reine grote terts C-E, en dan vanaf C een reine kwint naar G, en vanaf E een reine kwint naar A. De som van de kwinten G-D en D-A moet dan één syntonische komma afwijken. Verdeel de afwijking gelijk over deze twee kwinten (noot : hoe kan men dit doen), beiden worden dus een halve komma te klein. Verdeel nadien de bestaande afwijkingen gelijk tussen de kwinten C-G en G-D enerzijds, en ook tussen de kwinten D-A en A-E anderzijds (noot : ook hier ; hoe kan men dit doen). Deze kwinten hebben aldus alle vier een gelijke vermindering, die dus 1/2 van 1/2 komma = 1/4 van een komma bedraagt.
        De procedure hierboven geeft dus een beschrijving hoe een komma binnen een grote terts in vier kan gedeeld worden. Hoe daartoe een gelijkheid in afwijking wordt bereikt, wordt niet vermeld. Indien een gelijkheid tussen kwinten moet tot stand gebracht worden, indien ze samen geen deel uitmaken van een reine grote terts, is bovendien in het geheel niet duidelijk, zeker niet op basis van de bovenstaande procedure.
        De verdeling van een komma kan gemakkelijk, ook op niet aangrenzende kwinten, indien ze uitgevoerd wordt op basis van een waarneming van gelijke frequenties van zwevingen. Op basis van de formule voor zwevingen van een kwint of kwart, en met de noot A3 op 220 Hz (dus voor A4=440 Hz) voor een reine grote terts, bekomt men een gelijke zweving van 2,21 zwevingen/s., indien er zoals het gebruikelijk is, auditief gestemd wordt op de noten die liggen tussen F3 (F van het 3-de octaaf) en F4 [Calvet, 2020]. De nagerekende verhoudingen van de vier kwinten die de grote terts C-E vormen liggen tussen 1,49438… en 1,49624…, met tussen beiden een verschil in verhouding van niet meer dan 1,00124… ; dit is met normale harmonische afwijkingen in snaren onmogelijk met een monochord vast te stellen.
        Bemerking : indien men de middentoon wenst te stemmen met de noot A als stemvork, kan men de bovenstaande procedure aanvangen met een reine grote terts op F en een gelijkaardige aanpassing van de hierbij betrokken kwinten.

Een middentoon gestemd met een reine terts op C-E, met gelijke zweving op de kwinten C-G, G-D, D-A, A-E, binnen het octaaf op < F3 >, kan bekomen worden door de oplossing van de volgende vergelijkingen :

Reine grote terts op C4 : A2 = 220

q = q_C = q_G = q_D = q_A

p_C

Verdere reine grote tertsen :

0 = p_G = p_D = p_A = p_E = p_Bb = p_Eb

Dit leidt tot volgende tabel :

Noot	F3	F#3	G3	G#3	A3	Bb3
Klassiek	176,00	183,90	196,77	205,61	220,00	235,40
Zweving	176,00	183,79	196,78	205,56	220,00	235,26
q	- 1,77	- 1,38	- 2,21	13,03	- 2,21	- 1,77
p ; m	0,00	22,06	0,00	24,67	0,00	0,00

B3	C4	C#4	D4	Eb4	E4	F4
245,97	263,18	275,00	294,25	314,84	328,98	352,00
245,98	263,12	275,00	294,07	314,85	328,89	352,00
- 2,76	-2,21	- 2,76	- 2,21	- 3,54	-2,76
29,62	0,00	33,00	0,00	0,00	0,00	m = 133

Kwart komma Middentoon

De verschillen in toonhoogte tussen het “klassiek” berekend temperament en dit dat steunt op gelijke zwevingen, zijn onbeduidend, gemiddeld 0,16 cent, met een maximum gelijk aan 1,03 cent.
 Uit de tabel blijkt duidelijk, dat de zwevingen op de kwinten op C, G, D, A éénzelfde frequentie hebben, - 2,21 zwevingen/sec.. Om deze zweving precies in te stellen, kan er gebruik gemaakt worden van een metronoom ingesteld op 133. Nadat C, G, D, A en E zijn ingesteld, kan er verder auditief gestemd worden door het instellen van reine grote tertsen op F, G, D, A, E, Bb.
 De grote terts toonaarden in Bb, F, C, G, D, A hebben allen een identieke diatonische structuur en zijn zeer rein. De kwint op G# is zeer onrein, het is een wolfskwint. De vier grote tertsen op B, F#, C# en G#, die de grote kwint op G# omspannen, zijn eveneens zeer onrein. Daardoor zijn de toonaarden met drie of meer < # > of twee of meer zeer onrein, en er wordt normaal vermeden om deze toe te passen.
 De onreinheden van de middentoon en zijn minder bruikbare toonaarden kunnen ingezet worden voor het uitdrukken van hevige affecten. Sterke voorbeelden hiervan komen voor in de “Mattheus Passie” van J.S. Bach (zie Kelletat, 1982) tijdens de volgende sequenties : "Sind Blitze, sind Donner (het dondert en bliksemt)", … "Eröffne den feurigen Abgrund, o Hölle (open de vurige afgrond, oh hel)“, … "Der du den Tempel Gottes zerbrichts (Jij die de tempel van God vernietigt)“, … "Laß ihn kreuzigen (Laat hem gekruisigd worden)“, …"Ich bin's, ich sollte büßen (Ik ben het, ik moet boeten)“, … "Ach Golgotha, unselges Golgotha (O Golgotha, onzalige Golgotha)“, … "Wahrlich, dieser ist Gottes Sohn gewesen (Voorwaar, dit was de Zoon van God)“. Ook G.F. Händel en anderen hebben deze middentoon eigenschap gebruikt. W.A. Mozart daarentegen heeft maar sporadisch gebruikt gemaakt van de grote terts tonaarden in E of Eb de eerste toonaarden die tegen de goed klinkende toonaarden aanleunen, en heeft geen verder verwijderde toonaarden toegepast.
 Op de noten Eb, Bb, F, C, G, D, heeft men een redelijk consonante tritonus (van - 2,10 tot - 3,98 zwevingen/sec.). Alleen deze middentoon heeft zes consonante tritoni. Deze komen allen voor in Bach composities [Kelletat, 1960, 1981, p.45-46]. Dit is niet echt verwonderlijk, want Bach stond open voor elk interval dat goed klonk, en hij heeft veel met de middentoon gewerkt [Kelletat, 1960, 1981, p. 23], voornamelijk op orgels dus, die in zijn tijd meestal in middentoon gestemd werden.

1/5 Komma MIDDENTOON ; Sauveur (1701), Rossi (1666) (Terug naar Inhoud)

De kwart (1/4) komma middentoon heeft een sterke wolfskwint. De dissonantie van deze kwint kan verminderd worden door de grote tertsen een kleinigheid te vergroten, ze worden dus iets groter dan rein. Dit is mogelijk volgens de procedure voor de kwart komma middentoon, maar waarbij men door opeenvolgende benaderingen met kleine vergrotingen van de grote terts, komt tot op een punt dat de grote terts en de vier kwinten even snel zweven ; let wel, de grote terts zweeft dan wegens 1/5 komma te groot, en de kwinten zweven dan wegens 1/5 komma te klein.
(noot : 1/5+1/5+1/5+1/5+1/5 = 1).

De toonhoogtes kunnen zeer eenvoudig op basis van volgende vergelijkingen bekomen worden :

Gelijke zweving op kwinten en tertsen : A2 = 220

- q_C = - q_G = - q_D = - q_A = p_C = p_G = p_D = p_A = p_E = p_F = p_B_b = p_Eb

De oplossing ziet er uit als volgt

Noot	F3	F#3	G3	G#3	A3	Bb3
Klassiek	175,56	184,25	196,53	206,25	220,00	234,57
Zweving	175,61	183,98	196,64	205,88	220,00	234,80
q	- 1,17	- 0,97	- 1,95	10,81	- 1,65	- 1,95
p ; m	1,95	19,27	1,95	21,90	1,95	1,95

B3	C4	C#4	D4	Eb4	E4	F4
245,97	262,69	275,68	294,06	313,54	329,18	351,13
246,28	262,83	275,49	293,98	314,23	329,03	351,22
- 2,92	- 1,95	- 2,92	- 1,95	- 3,50	- 1,95	- 2,34
25,50	1,95	27,45	1,95	1,95	1,95	117

1/5 komma Middentoon

De verschillen in toonhoogte liggen iets boven de meestal waargenomen verschillen : 1,8 cents gemiddeld, met een maximum van 3,8 cents.

SILBERMANN (1/6 komma middentoon) ; Romieu (1758)(Terug naar Inhoud)

De 1/6 komma middentoon wijst op een verder evoluerende wens naar meer reinheid voor alle toonaarden.
        Silbermann was een zeer befaamd orgelbouwer ten tijde van J.S. Bach met wie hij ook bij de keuring van orgels heeft samengewerkt. Beklijvend is een uitspraak van Bach : hij zou aan Silbermann gezegd hebben dat deze zijn orgels stemt naar zijn wil, maar ook dat hij zelf muziek speelt naar zijn wil ; ... wat echter in het geheel niet betekent dat Bach het Silberman temperament niet goed zou gevonden hebben.
        De Silbermann orgels werden gestemd in middentoon waarbij de syntonische komma in zes gedeeld wordt, één stap verder dus in het verkleinen van de wolfskwint.
        De toonhoogtes kunnen zeer eenvoudig op basis van volgende vergelijkingen bekomen worden :

(Noot : 1/6+1/6+1/6+1/6+2/6=1)

De zweving op de grote terts is twee maal zo snel als deze op de kwinten : A2 = 220

- q_C = - q_G = - q_D = - q_A = 2p_C = 2p_G = 2p_D = 2p_A = 2p_E = 2p_F = 2p_Bb= 2p_Eb

De oplossing ziet er uit als volgt

Noot	F3	F #3	G3	G#3	A3	Bb3
Klassiek	175,27	184,48	196,37	206,68	220,00	234,18
Zweving	175,30	184,13	196,52	206,14	220,00	234,43
q	- 0,70	- 0,65	- 1,74	9,05	-1,74	- 2,09
p ; m	3,48	170,9	3,48	19,73	3,48	3,48

B3	C4	C#4	D4	Eb4	E4	F4
246,48	262,37	276,14	293.94	312.89	329,32	350,55
246,52	262,61	275,87	293,91	313,74	329,13	350,61
- 3,04	- 1,74	- 3,04	- 1,74	- 3,48	- 1,3	- 1,39
22,35	3,48	23,09	3,48	3,48	3,48	m = 104

Silbermann (1/6-de komma middentoon)

Met een metronoom op 104 heeft men 2 zwevingen per tik van de metronoom, op de kwinten binnen de grote terts < C-E >, en 4 zwevingen op alle grote tertsen. Ter controle heeft men ook 4 zwevingen op de kwint op Eb4.
De verschillen in toonhoogte liggen nog iets verder boven de meestal waargenomen verschillen : 2,3 cent, met een maximum gelijk aan 4,7 cent.
Men heeft nog andere middentoon temperamenten. Een hogere verdeling van de komma zal leiden tot verbetering van de kwinten tot op een punt dat ze allen bruikbaar worden, maar dit gaat natuurlijk ten koste van de kwaliteit van de tertsen.

WELGETEMPERD STEMMEN (ook welgetempereerd) (Terug naar Inhoud)

Kelletat geeft op basis van de publicaties van Werckmeister, een muzikale definitie voor het welgetemperd stemmen [1960 / 1981, p. 9 [ ⁶ ] ] :

“Welgetemperd stemmen veronderstelt een mathematisch-akoestische en praktisch-muzikale indeling van de tonen van een octaaf in twaalf delen, opdat er op basis van het rein systeem een onberispelijke uitvoering mogelijk zou zijn in alle toonaarden, waarbij dient gestreefd te worden naar een zo hoog mogelijke reinheid van de diatonische intervallen.
Dit temperament komt voor als een spaarzaam temperende, aan verhoudingen gebonden versoepeling en verlenging van het middentoonsysteem, als ongelijkzwevende halve tonen en als gelijkzwevend temperament.”

Voornamelijk in de Angelsaksische wereld worden Welgetemperde stemmingen ook circulaire temperamenten genoemd, -Circulating Temperament-, [Barbour, 1951, p. ix]. Deze naamgeving ondersteunt de karakteristiek dat alle kwinten op de kwintencirkel een aanvaardbare beperkte afwijking hebben. De maximaal toegelaten verminderde afwijking zou kunnen gesteld worden op een verhouding van ongeveer < 1,49 >, op basis van de verwerping door Marpurg [1776], van het Kirnberger II temperament dat kwinten A-E en D-A bevat met deze verhouding [Kelletat, 1960/81 ; p. 48] ; dit komt overeen met - 8,2 (A-E) en - 5,5 (D-A) zwevingen/sec. .
 Er zijn inderdaad grenzen aan het welgetemperd zijn.
 Een eerste uiterste grens wordt bereikt met de Gelijkzwevende Stemming. Indien men buiten de diatonische kwinten op C-groot, al was het maar één kwint zou hebben die kleiner is dan deze van de gelijkzwevende stemming, dan zou er binnen C-groot omwille van het sluiten van de kwintencirkel minstens één kwint moeten zijn die groter is dan deze van de gelijkzwevende stemming ; in andere woorden, er moet dan een diatonische ladder bestaan die reiner is dan deze van C-groot, en dit kan niet de bedoeling zijn.
 Twee andere uiterste grenzen worden bereikt wanneer de diatonische toonladder op C-groot één reine grote terts inhoudt. Een tweede reine grote terts is niet mogelijk, want hij leidt er mathematisch toe dat er dan buiten deze toonladder kwinten zullen zijn die groter zijn dan rein, en ook dit kan niet de bedoeling zijn. De twee bijkomende uitersten zijn aldus :

een reine grote terts op F, wat vier kwinten vereist die een syncopische komma verkleind zijn, deze op F, C, G, D, gecombineerd met een kwint op A die een schismatische komma verkleind is. De kwint op E en alle andere kwinten zijn dan rein
een reine grote terts op G, wat vier kwinten vereist die een syncopische komma verkleind zijn, deze op G, D, A, E, gecombineerd met een kwint op C die een schismatische komma verkleind is. De kwint op F en alle andere kwinten zijn dan rein.

De waarden van onreinheden van de kwinten en grote en kleine tertsen die met deze drie gevallen overeenkomen, kunnen in een lijngrafiek uitgezet worden, en hierdoor kunnen binnen deze lijnen de redelijk brede banden met de toegelaten minimum en maximum waarden van de onreinheden afgelezen worden.

Bovenste vlak : toegelaten gebied voor grote tertsen
Middenste vlak : toegelaten gebied voor kwinten
Onderste vlak : toegelaten gebied voor kleine tertsen

Het is duidelijk dat de toegelaten gebieden voor kwinten en grote en kleine tertsen enorm veel varianten toelaten. Daar is voornamelijk in de late Barok gretig gebruik van gemaakt.

WERCKMEISTER III [1691] (Terug naar Inhoud)

Welgetemperde toonladders worden onder deze naam vermeld door Werckmeister, door gebruik van de termen “wohl” en “temperieren”, weliswaar nog steeds niet als samengestelde term [Werckmeister, 1681, 1686, 1691, 1698]. Hieruit ontstond de term “Wohltemperiert”.
Het Werckmeister III temperament [1691, Cap. XXX, pp. 77-78], schrijft een vermindering voor met 1/4 komma, op de kwinten C-G, G-D, D-A, en B-F#. Alle andere kwinten worden verondersteld rein te zijn. Dit betekent dat de besproken komma in feite een pythagoreïsche komma moet zijn, en niet de syntonische komma, zoals verondersteld in zijn tekst. Bij verdeling van deze komma op basis van gelijke zwevingen, heeft men als criteria :
Één vierde van een komma :

q = q_C = q_G = q_D = q_B

Reine kwinten :

0 = q_A= q_F# = q_C# = q_G# = q_F = q_Bb =q_Eb

Men bekomt de volgende tabel.

Noot	F3	F#3	G3	G#3	A3	Bb3
Klassiek	175,60	185,63	196,89	208,12	220,00	234,14
Zweving	175,61	185,00	196,94	208,13	220,00	234,14
q	0	0	- 2,49	0	0	0
p ; r / m	1,96		5,31		- 2,94

B3	C4	C#4	D4	Eb4	E4	F4
247,50	263,40	277,50	294,33	312,18	330,00	351,21
247,50	263,41	277,50	294,16	312,19	330,00	351,22
- 2,49	- 2,49	0	- 2,49	0	0	0
- 14,19	2,94		- 8,89		- 10,62	m = 149

Werckmeister III

De verschillen in toonhoogte zijn miniem : minder dan 0,98 cent, gemiddeld 0,32 cent.

KIRNBERGER III (Terug naar Inhoud)

Kirnberger was een leerling van J.S. Bach, en heeft in 1771 “Die Kunst des reinen Satzes in der Musik” gepubliceerd. C.P.E. Bach, zoon van J.S. Bach, verdedigt het werk van Kirnberger als reactie op uitlatingen van Marpurg [Kirnberger, 1771, vol. II, deel III, p. 188 [ ⁷ ] ] :

“Het gedrag van meneer Marpurgen jegens u is verachtelijk. ….. Je kunt hardop zeggen dat de principes van mij en die van mijn vader anti-rameauïsch zijn”

C.P.E. Bach, beschrijft [1753] kwalitatief, - niet kwantitatief dus -, hoe men de kwinten licht afwijkend van de reinheid moet stemmen, gepaard aan een auditieve controle van grote en kleine tertsen, en volledige akkoorden, zó dat men in alle vier en twintig toonaarden rein kan spelen. Het is door de beschrijving duidelijk dat het een zuiver auditieve wijze van stemmen betreft. Het Kirnberger III temperament vertoont deze beschreven karakteristieken.
Forkel [1802, p. 41 [ ⁸ ]], een vriend van de zonen van Bach, getuigt dat zijn zonen nooit ontkenden dat de leer van Kirnberger in lijn ligt met deze van Bach, en getuigt zelf :

“Wie de reikwijdte van Bachs lesmethode op het gebied van compositie wil leren kennen, vindt deze in Kirnbergers “Kunst des reinen Satzes” adequaat uitgelegd.”

Een eerste temperament dateert van 1766. Zijn derde hieronder, wordt in 1779 beschreven in een brief aan Forkel. Volgens Kelletat [1960/81] zou dit mogelijk het temperament zijn dat door J.S. Bach werd toegepast voor de uitvoering van “Das wohltemperirte Clavier” (1722 / 1742-44), maar dit kan betwijfeld worden, want dit muziekwerk werd gepubliceerd lang vóór het eerste temperament van Kirnberger of ook de brief aan Forkel. Het feit dat de publicatie van Kirnberger in lijn ligt met de leer van Bach, impliceert niet noodzakelijk dat het temperament dat hij heeft ontwikkeld deze leer niet ondersteunt. Bach was niet begaan met de mathematische aspecten van het temperen bij het stemmen. Wel is bekend dat hij zeer bedreven was in het stemmen van zijn klavier, en dat in zeer korte tijd gedaan kreeg. Het stemmen moet dus relatief eenvoudig geweest zijn. Hier kan er op gewezen worden dat Kirnberger III zeer eenvoudig te stemmen is, maar dit belet niet dat er ook andere temperamenten zijn die aan deze eis kunnen beantwoorden, zoals er verder zal kunnen vastgesteld worden bij Vallotti en een nieuw voorstel dat op zijn beurt ook opnieuw steunt op verregaande gelijkheid van zwevingen.
Kirnberger III heeft een zeer eenvoudige structuur en behoort daardoor tot de meest gemakkelijk auditief te stemmen temperamenten. Karakteristieken zijn:

En reine grote terts op C

p_C = 0

Gelijke verdeling van de kwinten op C, G, A, E, die de grote terts op C samenstellen

q = q_C = q_G = q_D = q_A

Alle resterende kwinten rein, behalve deze op F#, die dus een schismatische komma verkrijgt

0 = q_E = q_B = q_C# = q_G# = q_F= q_Bb =q_Eb

Dit geeft volgende tabel.

Noot	F3	F#3	G3	G#3	A3	Bb3
Klassiek	175,45	185,05	196,77	207,95	220,00	233,94
Zweving	175,41	185,00	196,78	207,89	220,00	233,88
q	0	- 0,63	- 2,21	0	- 2,21	0
p; r / m	2,95		2,76		- 4,42

B3	C4	C#4	D4	Eb4	E4	F4
246,73	263,18	277,26	294,25	311,92	328,98	350,91
246,67	263,12	277,19	294,07	311,84	328,89	350,82
0	- 2,21	0	- 2,21	0	0	0
- 9,67	0		- 10,32		- 10,32	m=133

Kirnberger III

De verschillen in toonhoogte zijn miniem en gemiddeld gelijk aan 0,14 cent, met een maximum van 1,03 cent.

VALLOTTI (Terug naar Inhoud)

Het Vallotti temperament dateert uit 1728 en wordt door Tartini vermeld [1754]. Hij publiceert een eerste deel van een boek [1779], maar het is pas het tweede deel ervan, dat de beschrijving van zijn temperament bevat [1950, p. 192 e.v.], en dat klaar was voor publicatie, maar pas in 1950 werd gepubliceerd.
Vallotti stelt volgens de uitgave van 1950 voor om op basis van muzikale bedenkingen elk van de zes kwinten binnen de diatonische toonaard in C-groot te verminderen met een zesde van een syntonische komma, dit zijn de kwinten op F, C, G, D, A, E. De resterende zes kwinten worden rein verondersteld. Dit voorstel houdt een niet expliciet vermelde verwaarlozing in, van een schismatische komma. Zijn voorstel wordt daarom meestal geïnterpreteerd als een eis die in werkelijkheid neerkomt op een verdeling van de pythagorische komma, in plaats van de syntonische. Op deze basis bekomt men de berekening van zijn temperament zeer eenvoudig met :

Verminderde kwinten :

q = q_F = q_C = q_G = q_D = q_A = q_E

Reine kwinten :

0 = q_B = q_F# = q_C# = q_G# = q_Bb = q_Eb

Door bovenvermelde structuur valt het Vallotti temperament ook zeer gemakkelijk auditief te stemmen.

Men bekomt de volgende tabel.

Noot	F3	F#3	G3	G#3	A3	Bb3
Klassiek	175,40	184,79	196,44	207,89	220,00	233,87
Zweving	175,49	184,88	196,44	207,99	220,00	233,99
q	- 1,59	0	- 1,59	0	- 1,59	0
p ; r / m	2,54		3,85		- 7,77

B3	C4	C#4	D4	Eb4	E4	F4
246,38	262,51	277,18	294,00	311,83	329,26	350,81
246,51	262,45	277,32	293,86	311,99	329,21	350,99
0	- 1,59	0	- 1,59	0	- 1,59
- 9,74	4,60		- 8,25		- 10,87	m=95

Vallotti

De verschillen in toonhoogte zijn miniem en gemiddeld gelijk aan 0,72 cent, met een maximum van 1,70 cent.

NEIDHARDT 1 (Terug naar Inhoud)

Het loont de moeite ook na te gaan hoe gelijk de temperamenten zijn, in het geval van een meer ingewikkelde structuur. Neidhardt heeft zeer veel temperamenten voorgesteld, en zijn eerste voorstel bevat reine kwinten, en kwinten met verminderingen van 1/6 en zelfs 1/12 (!) komma, waarbij gelijkaardige kwinten niet steeds met elkaar aansluiten ; hoe dit moet uitgevoerd worden is niet meteen duidelijk. Dit leidt tot volgende berekening :
Drie kwinten, op C, G, D, verminderd met 1/6 komma

2q = q_C = q_G = q_D

Zes kwinten, , op A, B, F#, C#, Bb, Eb, verminderd met 1/12 komma

q = q_A = q_B = q_F# = q_C# = q_Bb = q_Eb

Drie reine kwinten

0 = q_F= q_E = q_G#

Men bekomt :

Noot	F3	F#3	G3	G#3	A3	Bb3
Klassiek	175,01	185,00	196,44	207,77	220,00	233,61
Zweving	175,00	185,19	196,46	207,83	220,00	233,60
q	0	- 0,82	- 1,63	0	- 0,82	- 0,82
p ; r / m	5,01		6,45		- 7,52

B3	C4	C#4	D4	Eb4	E4	F4
247,08	262,51	277,03	294,00	311,83	329,44	350,02
247,19	262,50	277,38	293,88	311,74	329,59	350,00
- 0,82	- 1,63	0	- 1,63	- 0,82	0	0
- 13,77	5,88		- 13,29		- 12,91	m=98

Neidhardt 1

De verschillen in toonhoogte zijn miniem en gemiddeld gelijk aan 0,93 cent, met een maximum van 1,70 cent.

BACH; DE WELGETEMPERDE MIDDENTOON (Terug naar Inhoud)

Het temperament dat J.S. Bach zélf effectief stemde op zijn klavecimbel, blijft een zeer speculatief onderwerp, waarop wellicht nooit een objectief en universeel aanvaard antwoord zal kunnen worden gegeven.

Ongeveer twee eeuwen lang, wellicht op basis van een publicatie van Marpurg [1776], werd aangenomen dat J.S. Bach het gelijkzwevend temperament heeft toegepast. Na een publicatie van Kelletat [1960 ; 1981], groeien er hierover sterke twijfels, op basis van musicologische analyses steunend ook op talloze referenties naar historische publicaties. Kelletat werd hierin nochtans voorafgegaan door Bosanquet [1876] en Barbour [1951], die dit standpunt evenwel niet zo diep en uitgebreid hadden behandeld. Na een voorstel voor een “Bach-temperament” door Kelletat zelf [1966], volgen talloze andere voorstellen. Een niet limitatieve lijst zou kunnen zijn : Kellner [1977], Billeter [1979, 2008], Barnes [1979], Lindley [1994, 2006], Sparschuh [1998], Jira [2000], Zapf [2001], Francis [2004], Lehman [2005], Allain-Dupré [2005], Jobin [2005], O’Donnell [2006], Spanyi [2006], Interbartolo/Venturino [2007], Di Veroli [2008], Amiot [2008], Broekaert [2020], enz...
De meest betrouwbare bronnen, hoe Bach zijn klavier stemde, zijn wellicht een publicatie van zijn zoon [Bach C.P.E., 1753] en Forkel [1802], die bevriend was met zijn zoon, en ook nauwe contacten had met Kirnberger, een Bach-leerling.
Bach C.P.E. [1802, par. 14, p. 17-18, [ ⁹ ] ] :

“Beide soorten instrumenten moeten goed gestemd zijn, in die zin dat door het stemmen van de kwinten, kwarten, het testen van de kleine en grote tertsen en hele akkoorden, vooral de meeste kwinten zoveel van hun grootste zuiverheid verliezen dat het oor en jullie allemaal het nauwelijks opmerkt. Er kan goed gebruik worden gemaakt van vier en twintig toonsoorten. Door de kwarten uit te proberen heb je het voordeel dat je de noodzakelijke zweving van de kwinten duidelijker kunt horen omdat de kwarten dichter bij hun grondtoon staan dan de kwinten. Als de piano's op deze manier worden gestemd, kunnen ze terecht worden omschreven als de zuiverste instrumenten van allemaal vanwege de manier waarop ze worden bespeeld, in die zin dat sommige piano's zuiverder zijn gestemd maar niet worden bespeeld. Op de piano speel je alle vier en twintig toonaarden met gelijke helderheid, en het valt op dat ze in perfecte harmonie zijn, ondanks dat de harmonie door de omstandigheden meteen de geringste onzuiverheid ontdekt. Met deze nieuwe manier van temperen zijn we verder gekomen dan voorheen, hoewel het oude temperament (toegevoegde noot : de middentoon) zodanig was dat sommige soorten tonen zuiverder waren dan je vandaag de dag nog steeds in veel instrumenten aantreft. …”

Forkel [1802, p. 41, [ ¹⁰ ] ] :

“Niemand kon hem bijstaan voor zijn vleugel. Hij deed het altijd zelf, stemde ook de vleugel en stemde zelf zijn klavichord, en was zo bedreven in dit werk dat hij er nooit meer dan een kwartier over deed. Maar toen hij fantaseerde, waren alle 24 sleutels van hem; hij deed met hen wat hij wilde. ...”

Bach zelf, was niet geïnteresseerd in toonverhoudingen, getallen en berekeningen rond temperamenten [Forkel, p. 39 [ ¹¹ ]].

“Hoe handig en veilig Bachs stijl van lesgeven ook was in het spel, zo was het ook in het componeren. Hij begon niet met droge, zinloze contrapunten, zoals het geval was bij andere muziekleraren van zijn tijd; Nog minder viel hij zijn studenten lastig met berekeningen van toonverhoudingen, die naar zijn mening niet aan de componist toebehoorden, maar louter aan de theoreticus en instrumentmaker.”

Op basis van het bovenstaande, zou het moeten duidelijk zijn, dat Bach auditief stemde. In de zoektocht naar het “Bach-temperament”, en zeker indien het besproken wordt op basis van zwevingen, wordt er dikwijls gerefereerd naar een gekrolde figuur die door Bach zelf op één van de partituren van “Das wohltemperirte Clavier” werd aangebracht. Zie het onderste gekrolde deel van de figuur hieronder.

In lijn met de meeste voorstellen, kan worden aangenomen dat de gelijke krollen die bij E4, A3, D4, G3, en C4 horen, overeenkomen met gelijk verminderde kwinten. Een eerste voorstel in die zin komt van Sparschuh [1999]. Jobin [2005] werkte hier ook een voorstel op uit, op basis van interval-verhoudingen, met twee reine grote tertsen, geinspireerd op de middentoon, die ten tijde van Bach zeer gebruikelijk was.
Jobin ligt aan de bron van het voorstel hieronder, dat werd uitgewerkt samen met Calvet, een auditief stemmer, en Amiot, professor wiskunde en muzikant. De vermindering van kwinten leidt tot een verbetering van de betrokken grote tertsen. De uitersten in de aanpassing van de kwinten liggen tussen reine kwinten enerzijds, en reine grote tertsen anderzijds. Onder de talloze mogelijkheden bij het welgetemperd stemmen, zou men als compromis bijvoorbeeld een gelijke onreinheid kunnen wensen voor kwinten en grote tertsen. Indien men zoals bij de middentoon begint met het stemmen van de grote terts C-E, dan moet er voor een gelijkheid van absolute waarden van onreinheden voldaan worden aan (let op het verschil in teken voor q en p ; normaal zijn kwinten iets te klein, en grote tertsen iets te groot) :

p = - q = p_C = p_G = p_D = p_A = p_E = - q_C

Het oplossen van dit stelsel leidt tot de vaststelling dat ook de onreinheid van de grote terts op G dezelfde onreinheid heeft. Analyse van het bovenstaande stelsel toont aan dat deze bijkomende gelijkheid een exact mathematisch feit is, want bovenstaand stelsel waaraan de gelijkheid < q_C = q_G > wordt toegevoegd blijkt redundand te zijn.
Bepaling van de noot < F >. Ook hier heeft men opnieuw de vrijheid om te kunnen zoeken naar een vergelijk tussen een reine kwint en een reine grote terts op < F >. Gelijkheid van de kwint met de reeds bestaande kwinten kan worden uitgesloten, omdat deze op de figuur niet wordt aangegeven. Een reine kwint op < F > is ongunstig voor de grote terts op < F >. Een mogelijke optie kan daarom zijn om de grote terts op < F > gelijk te maken aan de reeds uitgewerkte grote tertsen op < C > en < G >, zoals het in de middentoon gebruikelijk is, zodat :

p_F = p_C = p_G

waardoor de noot < F > is bepaald, en impliciet ook de kwint er op.
In lijn met veronderstellingen van Jobin en mogelijk ook andere “Bach-temperament” bedenkers, worden de kwinten op B, F#, C# rein, en wordt de < positieve ! > uiterst kleine overblijvende onreinheid verdeeld over de kwinten op < G# >, < Eb > en , < Bb >, mathematisch uitgedruk door :

0 = p_B = p_F# = p_C#

p_G# = p_Eb =p_Bb

Dit leidt tot de volgende tabel

Noot	F3	F#3	G3	G#3	A3	Bb3
Zweving	175,61	184,71	196,64	207,80	220,00	234,02
q	- 1,17	0	1,95	0,39	- 1,95	0,39
p ; r / m	1,95		1,95		- 5,84

B3	C4	C#4	D4	Eb4	E4	F4
246,29	262,83	277,07	293,98	311,90	329,03	351,22
0	- 1,95	0	- 1,95	0,39	- 1,95	- 2,34
- 7,79	1,95		- 7,79		- 7,79	m=117

Welgetemperde Middentoon

Let op de bekomen gelijkheid van de gewenste en aangeduide acht intervallen.
 Het verloop van de kwinten wordt op de voorgaande figuur met Bach-krollen, weergegeven met een lijn en ook bij middel van waarde-balken, en deze elementen hebben een mooie correspondentie met deze krollen.
 Het stemmen dat start met een gelijke zweving voor de grote terts C-E en de hierbij betrokken kwinten, en de < C > die getekend staat bij de krul voor < C4 > laten vermoeden dat de voor deze stemwijze gebruikte stemvork de noot < C > was, hoewel het stemmen evengoed mogelijk is vertrekkend van de < A > noot.
 De tritonus op F is redelijk consonant : - 2,14 zwev./sec, en komt voor in composities van Bach [Kelletat, 1960, 1981, p. 45-16].
 Het temperament valt auditief vlot te stemmen, en dit is volgens Forkel kenmerkend voor het gemak waarmee Bach stemde.
 De karakteristieken zijn ook op een kwintencirkel gemakkelijk af te lezen.

Welgetemperde Middentoon
Intervallen met < = > : - (kwinten) + 1.95 (grote tertsen) zw/s.
Intervallen met < 0 > : rein
Intervallen met < | > : + 0.39 zwevingen / sec.
Kwint op F : residuele waarde ~ - 1,17 zw/s.

Omwille van de opbouw van het temperament, waarbij een aanvakelijk op < C > bekomen grote terts verder gezet wordt op < F > en < G >, kreeg dit temperament als naam de “Welgetemperde Middentoon”, in samenspraak tussen de heren A. Calvet, E. Amiot en de auteur, personen die bij het tot stand komen van het temperament waren betrokken.
Het stemmen van dit temperament wordt uitgelegd op de website < https://www.youtube.com/watch-v=lwfESoMxd8Y >,

OPTIMALISATIE van een WELGETEMPERD KLAVIER (Terug naar Inhoud)

MINIMALISATIE van ONREINHEDEN (Terug naar Inhoud)

Bovenstaand werden een reeks belangrijke typische temperamenten berekend. Het is duidelijk geworden dat het rekenen met zwevingsfrequenties een zinvolle benadering is om temperamenten te karakteriseren, en dat er geen beduidende, laat staan meetbare, verschillen zijn met de toonhoogtes bekomen bij middel van verhoudingen of cents. Veel historische temperamenten zijn aldus meestal proefondervindelijk tot stand gekomen, met een wens tot uitgebalanceerde welluidendheid, zonder dat dit objectief met voldoende precisie kon gemeten worden.

1. Minimalisatie van de onreinheid van ALLE kwinten en tertsen binnen de diatonische C-groot toonaard.

Op basis van de bevindingen zou een mogelijk criterium om een “optimaal” wel getemperde stemming te bekomen kunnen inhouden dat er een minimum aan zwevingen gewenst wordt. Dit criterium is gemakkelijk mathematisch te bepalen als minimum van de som van alle zwevingen op de belangrijkste diatonische intervallen binnen C-groot : zes winten, drie grote tertsen en vier kleine tertsen.

In eerste instantie werd de minimalisatie ooit bepaald door opeenvolgende iteraties. Deze iteraties werden niet uitgevoerd bij middel van een specifiek daartoe geschreven programma, doch wel manueel in een standaard rekenblad. Deze procedure is zeer arbeidsintensief en tijdrovend, wil men komen tot een uitslag die precies is tot op 1/100 Hertz. Dank zij een advies van prof. E. Amiot werd de berekening van een minimum objectiever, eenvoudiger, sneller en precieser.

De som hierboven, wordt na uitwerking :

Het minimum van deze som kan worden bepaald, door het uitwerken van haar partiële afgeleiden naar de zes onbekende noten F, C, G, G, E, B.

De aan nul gelijk gestelde partiëlen van de bovenstaande som, vormen na vereenvoudiging van de coëfficienten, een stelsel van zes lineaire vergelijkingen met zes onbekenden ; perfect oplosbaar dus (Cramer, 1750, p. 59-60, App. No.1, p. 657-659).

	F3	C4	G3	D4	E4	B3	=	A3
δΣ/δF3	67	- 3	0	- 30	0		=	10
δΣ/δC4	- 6	63	- 12	0	- 20	0	=	30
δΣ/δG3	0	- 6	75	- 3	- 30	- 10	=	0
δΣ/δD4	- 30	0	- 3	37	0	- 15	=	6
δΣ/δE4	0	- 20	- 60	0	65	- 12	=	6
δΣ/δB3	0	0	- 10	- 15	- 6	34	=	0

Verder kunnen de vijf gewijzigde noten, bekomen worden door eenvoudige gelijkstelling van de zweving van hun kwinten. Men bekomt aldus als oplossing van het geheel aan vergelijkingen :

Noot	F3	F#3	G3	G#3	A3	Bb3
Zweving	176,47	184,66	197,14	208,34	220,00	234,97
q	- 2,43	0,95	- 2,57	0,95	- 2,49	0,95
p	- 2,34	16,60	- 2,14	12,27	9,86	2,85
r	- 17,13	- 7,95	- 8,00	- 20,54	- 2,57	- 22,52

B3	C4	C#4	D4	Eb4	E4	F4
245,89	263,49	277,46	294,43	312,98	328,76	352,94
0,95	- 1,88	0,95	- 3,29	0,95	- 2,69	- 4,86
22,45	- 2,41	24,42	5,12	12,25	22,91	-4,68
- 3,22	- 16,02	- 21,01	- 1,90	- 31,29	- 1,09	- 34,25

Toonladder_1 met Minimale Zweving van diatonische intervallen

Deze oplossing omvat verminderde grote tertsen op F, C, G. De optimale vermindering van de onreinheid, inclusief deze van de kleine tertsen, leidt tot een ver doorgedreven vermindering van de kwinten, zo ver dat zelfs de diatonische grote tertsen verminderde tertsen worden. Verdere gevolgen hiervan zijn dat er zes redelijk sterk vermeerderde kwinten zijn, op B, F#, C#, G#, Eb, Bb, en dat er aan gepaarde grote tertsen groter dan pythagoreisch zijn, op E, B, F#, C#. Het is onwaarschijnlijk dat deze toonladder ooit muzikaal zal toegepast worden.
Bovendien is het auditief stemmen volgens deze toonladder niet eenvoudig : hoe kan men weten dat een optimum werd bereikt indien men dit niet berekende en niet kende : de bovenstaande berekening of redenering, of een benadering of toepassing ervan, werd tot nog toe niet teruggevonden in de literatuur.

2. Minimalisatie van de onreinheid van kwinten en alleen de grote tertsen binnen de diatonische C-groot toonaard.

Een herhaling van de bovenstaande procedure, met uitsluiting van kleine tertsen leidt tot volgende resultaten.
De som van de onreinheden, zonder met reine tertsen te rekenen, wordt na uitwerking :

som10

som11

som12

som13

som15

De aan nul gelijk gestelde partiëlen van de bovenstaande som, vormen na vereenvoudiging van de coëfficienten, een stelsel van zes lineaire vergelijkingen met zes onbekenden ; perfect oplosbaar dus.

	F3	C4	G3	D4	E4	B3	=	A3
δΣ/δF3	17	- 3	0	0	0		=	10
δΣ/δC4	- 3	19	- 6	0	- 10	0	=	0
δΣ/δG3	0	- 6	25	- 3	0	- 10	=	0
δΣ/δD4	0	0	- 6	13	0		=	12
δΣ/δE4	0	- 20	0	0	29	- 12	=	6
δΣ/δB3	0	0	- 5	0	- 3	8	=	0

Verder kunnen de vijf gewijzigde noten, bekomen worden door eenvoudige gelijkstelling van de zweving van hun kwinten. Men bekomt aldus als oplossing van het geheel aan vergelijkingen :

Noot	F3	F#3	G3	G#3	A3	Bb3
Zweving	176,86	184,98	197,08	208,24	220,00	234,40
q	- 1,19	0,22	- 3,16	0,22	- 1,89	0,22
p	0,72	12,71	0,89	11,56	10,32	4,12
r	- 13.,95	- 9,88	- 10,44	- 16,59	- 4,06	- 18,53

B3	C4	C#4	D4	Eb4	E4	F4
246,57	263,19	277,58	294,04	312,47	329,06	351,71
0,22	- 1,26	0,22	- 2,11	0,22	- 0,89	- 2,39
17,02	0,28	18,96	9,67	14,29	20,63	1,43
- 9,24	- 16,80	- 20,20	- 5,65	- 24,99	- 3,56	- 27,90

Toonladder_2 met Minimale Zweving van diatonische intervallen

Deze toonladder oogt veel beter dan de vorige. Ook hier kent men het minimum slechts na berekening, en de zwevingen van de kwinten verschillen nogal, zodat een voorschrift voor het auditief stemmen moeilijk te onthouden valt, en kennis en gebruik van een stemtabel dus vereist is. Ook hier kan men vaststellen dat de bovenstaande berekening of redenering, of een benadering of toepassing ervan, tot nog toe niet teruggevonden werd in de literatuur..

MINIMALISATIE van de SPREIDING van ONREINHEDEN (Terug naar Inhoud)

Behalve hierboven, gingen de voorgaande berekeningen van temperamenten in deze tekst allen voornamelijk terug op een gelijkheid van zwevingen. Vandaar dat men een optimalisatie zou kunnen wensen waarbij alle diatonische intervallen een zo gelijk mogelijke zweving zouden hebben. Een zo goed als mogelijke gelijkheid betekent een minimalisatie van de absolute waarden van de afwijkingen van een gemiddelde.

Dit is : Een minimalistie van de spreiding van de onreinheden

Voor een correcte analytische berekening dient er dus ook vooraf correct rekening te worden gehouden met de tekens van de afwijkingen. Bovendien dienen de kleine tertsen afzonderlijk te worden berekend op hun afwijking, gezien ze door hun grotere afwijkingen, - en ook door de zin waarin ze evolueren -, anders zouden kunnen leiden tot onaanvaardbare resultaten. Ook de niet-diatonische kwinten worden afzonderlijk behandeld. Al deze voorwaarden leiden tot de formules hieronder voor het berekenen van de afwijkingen van een gemiddelde onreinheid. Hieruit kan dan verder een correcte analytische berekening volgen op basis van de som van de kwadraten van deze afwijkingen :

Diatonische kwinten :

Diatonische grote tertsen :

Diatonische kleine tertsen :

Niet-diatonische kwinten :

Een eerste te minimaliseren expressie wordt aldus :

De som hierboven, wordt na uitwerking :

De gelijk aan nul gestelde partiële afgeleiden, worden na vereenvoudiging van de coëfficienten :

N	F3	4	G3	D4	E4	B3	=	A3
δΣ/δF3	1954	- 349	- 474	- 1031	290	270	=	7
δΣ/δC4	- 698	1979	- 978	61	- 370	270	=	76
δΣ/δG3	- 158	- 163	726	- 17	- 250	- 30	=	- 10
δΣ/δD4	- 2062	61	- 102	2651	- 74	- 1134	=	49
δΣ/δE4	- 290	- 185	- 750	- 37	958	- 378	=	30
δΣ/δB3	30	15	- 10	- 63	- 42	118	=	1

De oplossing van de vergelijkingen in bovenstaande tabel, dient te worden aangevuld met de eenvoudige berekening van gelijke zwevingsfrequenties op de niet diatonale kwinten, -het is niet nodig via de meer ingewikkelde gelijkheid van de verschillen in onreinheid van de kwinten te gaan-, en leidt tot de uitslag in de volgend tabel :

Noot	F3	F#3	G3	G#3	A3	Bb3
Zweving	175,66	184,67	196,56	207,94	220,00	234,12
q	- 1,71	0,29	- 1,78	0,29	- 2,42	0,29
p	1,70	13,09	1,75	10,83	8,63	5,20
r	- 14,25	- 8,04	- 8,77	- 16,97	- 6,84	- 18,91
cents	10,33	- 3,03	4,95	2,40	0,00	7,66

B3	C4	C#4	D4	Eb4	E4	F4
246,13	262,63	277,16	293,94	312,06	328,79	351,32
0,29	- 1,66	0,29	- 1,83	0,29	- 1,83	- 3,43
17,55	1,99	19,49	7,67	12,19	19,58	3,41
-7,09	- 15,51	- 19,00	- 7,07	- 25,60	- 7,15	- 28,51
- 5,67	6,65	- 0,16	1,65	5,17	- 4,41	10,33

Toonladder met minimum spreiding van zwevingen op diatonische intervallen

Een aantal intervallen met quasi gelijke zwevingsfrequentie kunnen worden waargenomen. Er mag aldus verwacht worden dat een professionele stemmer in staat is om dit temperament op het oor te kunnen instellen, waarbij de zwevingsfrequentie van de diatonische kwinten en grote tertsen rond 1,85 ligt, hierbij natuurlijk rekening houdend met het vereist teken. Dit is op het oog zeer goed vergelijkbaar met het “Bach”-temperament (8 intervallen op - 1,95) en Vallotti (6 kwinten op - 1,59).

OPTIMALISATIE VAN EEN WELGETEMPERD KLAVIER (Terug naar Inhoud)

op basis van INTERVAL VERHOUDINGEN of CENTS

Een belangrijke kritiek op het uitwerken van een optimaal welgetemperd temperament, op basis van zwevingsfrequenties van intervallen, zou kunnen inhouden dat het streven naar minimum spreiding van zwevingsfrequenties geen rekening houdt met de toonhoogte van de grondnoot van een interval ; het zou beter en logischer kunnen zijn dat intervallen op hogere toonhoogtes inderdaad proportioneel hogere zwevingsfrequenties zouden hebben. Het is daarom zinvol om het toegepaste reinheidscriterium ook te evalueren, indien gebaseerd op “klassiek” uitgedrukte onzuiverheden in verhoudingen of cents, in plaats van op zwevingsfrequenties.
Dank zij de evenredigheid van onreinheden worden de berekeningen zeer eenvoudig. Onafhankelijk van hun toonhoogte zien we dat gelijke diatonische onreinheden op kwinten leiden tot er aan gepaarde gelijkheden van de kwinten op zich, en dus ook tot volmaakte gelijkheden binnen de groep van de diatonische grote tertsen en kleine tertsen die er mee betrokken zijn. De enige voorwaarde die daarom moet worden gesteld, vereist de gelijkheid van de onreinheden van diatonische kwinten en grote tertsen in absolute waarden. Dit kan binnen de toonladder op C-groot worden uitgedrukt door :

Gelijkheid van de onreinheden :

gecombineerd met de onderstaande voorwaarde, dat vier kwinten min twee octaven, eindigen op een grote terts : eenvoudiger gezegd betekent dit dat een grote terts opgebouwd is met vier kwinten.

Of, na vereenvoudiging :

Bijgevolg :

kwint = 1,49627787 …

grote terts = 1,25310949 …

De zes resterende kwinten, hier < kwint_alt > genoemd, kunnen gelijk zijn, en moeten daarom voldoen aan:

en dus

Bekomen temperament :
(de onreinheden p, q, r worden hier in cents uitgedrukt)

Noot	F3	F#3	G3	G#3	A3	Bb3
Cents	175,56	184,75	196,53	207,93	220,00	234,03
Zweving	175,66	184,67	196,56	207,94	220,00	234,12
q	- 4,30	0,39	- 4,30	0,39	- 4,30	0,39
p	4,30	23,07	4,30	18,38	13,69	8,99
r	- 22,68	- 13,30	- 13,30	- 22,68	- 8,60	- 22,68
cents	9,39	- 2,35	4,69	2,35	0,00	7,04

B3	C4	C#4	D4	Eb4	E4	F4
246,27	262,69	277,18	294,06	311,97	329,18	351,13
246,13	262,63	277,16	293,94	312,06	328,79	351,32
0,39	- 4,30	0,39	- 4,30	0,39	- 4,30	- 4,30
23,07	4,30	23,07	8,99	13,69	18,38	4,30
- 8,60	- 17,99	- 17,99	- 8,60	- 22,68	- 8,60	- 22,68
- 4,69	7,40	0,00	2,35	4,69	- 2,35	9,39

Toonladder met minimum cents spreiding van diatonische intervallen

De verschillen tussen de hier gegeven “Cents”, en de voorheen bepaalde “Zweving”, liggen iets hoger dan gewoonlijk bij voorgaande vergelijkingen tussen temperamenten. Toch zijn de verschillen nog klein : gemiddeld 0,81 cent, met een maximum van 2,06 cent.

EVALUATIE VAN ONREINHEDEN (Terug naar Inhoud)

Hoewel het niet eenvoudig is om een alomvattend algoritme te definiëren voor de evaluatie van temperamenten [Hall D.; p. 275-277], worden hieronder een aantal temperamenten vergeleken, op basis van de spreiding van de reinheidsverschillen van kwinten, en grote en kleine tertsen ; dit criterium werd in deze tekst inderdaad toegepast om een welgetemperd temperament te definiëren dat optimaal is op gebied van gelijkheid van de onreinheden van de diatonische intervallen van de C-groot toonaard.
Deze spreiding van onreinheden kan worden berekend op basis van de frequenties van zwevingen op intervallen, maar ook op basis van interval afwijkingen in cents. Ze worden verder berekend voor een aantal temperamenten, met onderstaande formule, toegepast binnen de F3 – E4 partitie :

Opmerkingen:
Voor de berekening van een “gestandaardiseerde” “diatonische reinheidsspreiding” op basis van de zwevingen van de intervallen, voor andere tonaliteiten dan C-groot, moet de waarde van de stemvork gelijk zijn aan de toonhoogte van de sext van die tonaliteit.
De term 220/Stemvork moet worden verwijderd voor berekeningen op basis van cents.

Doel van de berekening is vast te stellen welke historische temperamenten het best overeenkomen met het hier gesteld reinheids criterium. Resultaten voor andere temperamenten zijn zo nodig gemakkelijk bijkomend na te rekenen. Een aantal bekomen spreidingswaarden voor zwevingen en voor cents, worden in de tabel hieronder opgegeven.

Bij deze tabel dient te worden opgemerkt :

Temperamenten die met < (bach) > zijn gemerkt werden ooit geclaimd als door J.S. Bach toegepast.
Temperamenten die met < bps > zijn gemerkt, zijn herberekende temperamenten, op basis van een gelijkmatige verdeling van de komma, berekend op basis van zwevingen in plaats van verhoudingen of cents.
In beide kolommen staan de Welgetemperde Middentoon en Vallotti samen op de eerste plaatsen, bovenaan in de tabellen.

Doordat de Welgetemperde Middentoon en het Vallotti temperament samen bovenaan in de tabellen te staan, zou een met Vallotti gestemd klavier vandaag de dag wellicht de beste indicatie kunnen zijn van hoe “Das wohltemperirte Clavier” van J.S. Bach in zijn tijd zou hebben kunnen klinken, ... mocht de Welgetemperde Middentoon inderdaad ooit door Bach gebruik geweest zijn.

Spreiding van zwevingen		Spreiding van cents
Minimale zwevingsspreiding	0.161	Minimale cent spreiding	0.000
Welgetemperde middentoon (bach)	0.436	Vallotti - Tartini	0.922
Minimale cent spreiding	0.696	Welgetemperde middentoon (bach)	1.304
Vallotti bps	0.940	Minimale zwevingsspreiding	1.388
Vallotti - Tartini	0.960	Vallotti bps	1.738
Barca (Devie)	1.247	Barca (Devie)	1.840
Mercadier bps	1.268	Mercadier bps	2.792
Kirnberger III bps (bach)	1.427	Neidhardt-1	3.351
Kellner bps (bach)	1.450	Jobin (bach)	3.488
Kirnberger III (bach)	1.457	Kirnberger III (bach)	3.740
Jobin (bach)	1.504	Kirnberger III bps (bach)	3.862
Neidhardt-1	1.582	Kellner bps (bach)	3.933
Werckmeister III	2.208	Vincentio Galilei 12-TET	5.530
Werckmeister III bps	2.247	Werckmeister III	5.672
Vincentio Galilei 12-TET	2.724	Werckmeister III bps	5.954

MINIMUM SPREIDING EIGENSCHAPPEN (Terug naar Inhoud)

ONREINHEID van DIATONISCHE KWINTEN, en GROTE en KLEINE TERTSEN (Terug naar Inhoud)

Bij de beoordeling van temperamenten, worden de onreinheden van kwinten, grote en kleine tertsen uitgedrukt in cents, dikwijls grafisch weergegeven bij middel van een lijn- of balkendiagramma. Doet men dit op basis van zwevingen, dan krijgt men ondulerende zaagtanden in de figuur, omdat de sequenties van quinten op de abcis dan leiden tot grote frequentiesprongen van de grondtonen van de intervallen, waardoor de grafieken moeilijker te interpreteren zijn. Daarom worden de grafieken voor een onderlinge grafische vergelijking van de “Minimum cent spreiding” met Vallotti en de “Welgetemperde Middentoon” ook hier weergegeven in cents in plaats van zwevingen. Men kan ook grafisch zien dat deze drie temperamenten zeer nauw bij elkaar aansluiten. Ter vergelijking zijn in dunne lijn ook karakteristieken van de middentoon, en het gelijkzwevend temperament weergegeven alsook het niveau van Pytharoreïsche tertsen.

Volle lijn : Minimale cent spreiding
Streeplijn : Vallotti
Streep-punt-lijn : Welgetemperde Middentoon

BELANG VAN DE HALFTONEN (Terug naar Inhoud)

Kelletat (1994) hecht in zijn publicaties alom zeer veel belang aan de halftonen, voor de klassieke zang. Hij vergelijkt de karakteristieken van de Kirnberger III halftonen ook met deze van de Middentoon, en besluit dat de Kirnberger III halftonen aanvaardbaar zijn. Hieronder een grafische vergelijking van deze halftonen, met deze van de Minimale Cent Spreiding. Voor de duidelijkheid van de grafiek zijn Vallotti en de Welgetemperde Middentoon weggelaten : ze verschillen haast niet.

Volle lijn : Kirnberger III

TONALITEIT (Terug naar Inhoud)

Een temperament met minimum spreiding werd bepaald, omdat dit tegemoet kan komen aan een optimalisatie op basis van auditieve waarnemingen, zonder enig hulpmiddel, en aldus zou kunnen stroken met wat een stemmer impliciet of intuïtief op het oor doet. De ganse problematiek is echter gestart bij de wens om de toonaard in C groot zo rein mogelijk te hebben. De kwadratisch gemiddelde reinheid van de kwinten, grote en kleine tertsen, van alle toonaarden werd berekend voor drie temperamenten : het temperament met optimale spreiding, in volle lijn hieronder, en de middentoon en de gelijkzwevende stemming, in streeplijn.

Op basis van de hierboven grafisch geïllustreerde karakteristieken van de toonaarden, wordt het overduidelijk, dat er grote verschillen zijn in het algemeen, tussen temperamenten, alnaargelang ze gelijkzwevend zijn, of bij de middentoon horen, of “welgetemperd”. Het streefdoel om een welgetemperde stemming te hebben, met een zo rein mogelijke toonaard voor C-groot, blijkt hier wellicht wel te zijn bereikt.

Deze “kwantitatieve” evaluatie van toonaarden, weerspiegelt in zekere mate mogelijke “kwalitatieve” indelingen door musici en musicologen ; een dergelijke indeling is bijvoorbeeld deze van Kirnberger (Kelletat, deel III, 199, pag. 89 ; Kirnberger, deel II, p. 74 e.v.), die de individuele muzikale karakteristieken van elke toonaard grondig bespreekt, en ze ook bondig groepeert in drie groepen volgens de tabel hieronder. Vergelijk de ligging van de toonaarden in de tabel, ook met hun ligging in de twee laatste grafieken hierboven :

Groep 1 heeft veruit de reinste diatonische intervallen.
Groep 2 heeft groeiende vergroting van de onreinheid van tertsen.
Groep 3 heeft de minst reine tertsen, zowel groot als klein

	Grote terts toonaarden	( = ) kleine terts toonaarden
1	F, C, G, D	d, a, e, b
2	A, E, B, F#	f#, c#, g#, eb (vgl. d#)
3	Db (vgl. C#), Ab (vgl. G#), Eb, Bb	bb, f, c, g

EEN ZWEVENDE MUSICOLOGIE (Terug naar Inhoud)

De ontleding van temperamenten op basis van zwevingen van intervallen heeft het mogelijk gemaakt om een aantal karakteristieken van temperamenten meer diepgaand te belichten. Ze ondersteunt de hypothese dat het auditief stemmen van een klavier vooral steunt op een subjectieve beoordeling - niet met apparaten gemeten dus -, naar gelijkheid van zwevingen op de belangrijkste diatonische intervallen.
        Deze ontleding heeft geleid tot een rationeel verklaarbaar en plausibel voorstel voor een temperament dat mogelijk door J.S. Bach zou zijn gestemd op zijn clavecimbel.
        Bovendien blijkt dat het hier voorgesteld Bach-temperament, - de welgetemperde middentoon -, en dat volgens Vallotti, beiden samen veruit de best geklasseerden zijn, indien beoordeeld vanuit het standpunt dat de onreinheden van de belangrijkste diatonische intervallen een zo klein mogelijke spreiding zouden moeten hebben.
        Zoals reeds gesteld : een volgens Vallotti gestemd klavier is zeer waarschijnlijk het klavier dat op zijn best weergeeft hoe “Das wohltemperirte Clavier” bij Bach zou hebben kunnen klinken.

Gelukkig kan er opgemerkt worden dat de verschillen in absolute toonhoogte en van karakteristieken in het algemeen, tussen temperamenten berekend op basis van verhoudingen, en deze berekend op basis van zwevingen, onbeduidend zijn. De verschillen zijn zo klein dat ze zeker niet meetbaar zijn met een monochord, waardoor ze in het verleden onopgemerkt bleven, en nu ook nog meestal, zelfs ook met meest moderne meetapparatuur. Er is dus gelukkig meestal ook geen herziening nodig van publicaties op basis van verhoudingen, alhoewel men bij sommigen soms een foutje kan waarnemen door het impliciet of onachtzaam negeren of vergeten van de schismatische komma, zoals werd opgemerkt voor Vallotti en Werckmeister III, - die nochtans zeer belangrijke temperamenten zijn -, en wellicht nog anderen.

Buiten het rationele binnen deze tekst, blijft het feit dat de keus van een temperament artistiek volledig vrij is en vrij blijft, en dat deze keus daardoor, indien er bewust moet gekozen worden, meestal kan en mag geschieden op artistieke gronden, zoals, periode of aard van het stuk, bespeeld instrument, gewenste affecten, componist, uitvoerend muzikant, enz. …

Het wordt wellicht alsmaar moeilijker om met volle zekerheid te kunnen blijven stellen dat het gelijkzwevend temperament de meest geschikt welgetemperde stemming is voor persoonlijke privé muziek praktijk van een zo breed mogelijk muziek repertorium. Wellicht is een goede welgetemperde stemming, bij uitstek Vallotti, meer of het meest geschikt, … het evenwaardig voorgesteld Bach temperament, - de welgetemperde middentoon -, is haast niet gekend en aanvaard, en tóch ook iets moeilijker te stemmen. Wel blijft er een kleine kans misschien dat het ooit doorbreekt bij gespecialiseerde didactische demonstraties?

Het Vallotti temperament kan naar believen zowel auditief als op basis van metingen worden aangebracht ; de verschillen zullen haast niet meetbaar zijn, ... en auditief met zekerheid niet waarneembaar.

BIBLIOGRAFIE (Terug naar Inhoud)

Aaron P. 1523 : “Toscanello in musica”.

Allain-Dupré P. 2005 : “Justesses et Tempéraments” (academia.edu) variation of Lehman’s proposal.

Amiot E. 2008 : “Discrete Fourier Transform and Bach’s Good Temperament” ; MTO, Volume 15, Number 2, June 2009

Bach C. P. E. 1753 : “Versuch über die wahre Art des Clavier zu spielen, mit Exemplen und achtzen Probe=Stücken in sechs Sonaten”.

Barbour J. 1951 : “Tuning and temperament : a historical survey”.

Barnes J. 1979 : “Bach's Keyboard Temperament: Internal Evidence from the Well-tempered clavier" ; EarlyMusic, Volume 7, Issue 2, April 1979, Pages 236–249,

Billeter B. 1979 : “Anweisung zum Stimmen von Tasteninstrumenten in verschiedenen Temperaturen” (ISBN 3-7537-160-7).

Billeter B. 2008 : "Zur 'Wohltemperirten' Stimmung von Johann Sebastian Bach: Wie hat Bach seine Cembali gestimmt-" ; (Ars Organi Zeitschrift, 2008-3, p. 18-21)

Blaumont N. 2012 : “Scènes et Coulisses” ; Ed. Versant Sud

Bononcini G.M. 1673 : “Musico prattico : Che brevemente dimostra il modo di giungere alla perfetta cognizione di tutte quelle cose, che concorrono alla composizione de i canti, e di ciò ch'all'arte del contrapunto si ricerca: Opera ottava”. 1673

Bosanquet R. 1876 : “An elementary treatise on Musical Intervals and Temperament”. Macmillan & Co. 1876

Broekaert J. 2020 : “Le Mésotonique Tempéré de Bach” (Pianistik No 111, dec. 2020, p. 4-19)

Calvet A. 2020 : “Le Clavier Bien Obtempéré” ISBN 978-2-9541401-3-1.

Cramer, G. 1750. Introduction à l'Analyse des Lignes Courbes Algébriques. Frères Cramer and Cl.

Di Veroli C. 2008 : “Unequal Temperaments: Theory, History and Practice” (e-book) The Viola da Gamba Society Journal, Volume Four, (2010)

Di Veroli, C. 2018. \Accurate Meantone Tuning based on Fogliano." Harpsichord and Fortepiano, Vol. 23, no. 1, pp. 16{20, United Kingdom 23: 19{20.

Euler, Leonhard (1739) : “Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae”. Sint Petersburg Academie.

Fletcher H., Stratton Richard, Blackham E. Donnell. 1962. “Quality of Piano Tones." The Journal of the Acoustical Society of America 34: 749-761.

Fogliano, L. 1529. Musica Theorica. G. A. Nicolini da Sabbio, Venezia, Italië.

Forkel J. 1802 : “Uber Johan Sebastian Bach’s Leben, Kunst und Kunstwerke”. Leipzig, Hoffmeister und Kuhnel. (Bureau de Musique). 1802.

Francis J. C. 2004 : “The Keyboard Temperament of J. S. Bach” (Eunomios).

Fritz B. 1757 : “Anweisung, wie man Claviere, Clavecins, und Orglen nach einer mechanischen Art, in alle zwölf Tönen gleich und rein stimme könne, daß aus solchen allen sowol dur als moll wohlklingend zu zpielen sein”. Leipzig 1757.

Galilei V. 1581 : “Dialogo di Vincentio Galilei . della musica antica, et della moderna”

Gerhard D., Hu H., 2019 : “Modelling 4-dimensional Tonal Pitch Spaces with Hopf Fibration”

Hall D., 1973 : “The Objective Measurement of Goodness-of-Fit for Tunings and Temperaments”, Journal of

Music Theory, Vol. 17. No. 2. (Autumn 1973)

Hans Schneider – Tutzing}. ISBN 3-79521-004-6).

Interbartolo G., Venturino P 2007 : Bach 1722 "Il temperamento de Dio". {ISBN A000068628).

ISO 16, 1975 : Acoustics, Standard tuning frequency (Standard musical pitch)

Jedrzejewski F. 2002 : “Mathématiques des systèmes acoustiques, Tempéraments et modèles contamporains”, 'Harmattan, Paris.

Jira M. 2000 : “Musikalische Temperaturen und Musikalischer Satz in der Klaviermusik von J. S. Bach” (2000,

Jobin E. 2005 : "BACH et le Clavier bien Tempéré" ; (website of "Clavecin en France").

Kelletat H. 1960 : “Zur musikalischen Temperatur”. Kassel, Oncken 1960

Kelletat H. 1966 : “Ein Beitrag zur musikalischen Temperatur der Musikinstrumente vom Mittelalter bis zur Gegenwart”. Reutlingen,

Kelletat H. 1981 : “Zur musikalischen Temperatur”; Band I. Johann Sebastian Bach und seine Zeit“. ISBN 3–87537 156–9

Kelletat H. 1982 : “Zur musikalischen Temperatur”. Band 2. Wiener Klassik”. ISBN 3-87537-187-9

Kelletat H. 1994 : “Zur musikalischen Temperatur” ; Band III. Franz Schubert”. ISBN 978–3–87537–239–5

Kellner H. 1977 : “Eine Rekonstruktion der wohltemperierten Stimmung von Johann Sebastian Bach“. Das Musikinstr. 26, 1977, 34-35

Kemp D.T. (1978) : “Stimulated acoustic emissions from within the human auditory system”. J Acoust Soc Am 64:1386–1391.

Kirnberger J. 1771 : “Die Kunst des reinen Satzes in der Musik”, ISBN 3-487-01875-6

Lehman B. 2005 : “Bach’s extraordinary temperament: our Rosetta Stone – 1 ; – 2” (Early Music, vol. 33, No 1,feb 2005, p.3-23 ; vol. 33, No 2, may 2005 p. 211-231).
Reaction : a number of letters are addressed to “Early Music” : Jencka D. (2005–8, p. 545) ; Maunder R. (2005–8, p. 545–546) ; Mobbs K., MacKenzie A. (2005–8, p. 546–547),

Lindley M. 1994 : "A Quest for Bach's Ideal Style of Organ Temperament" (M. Lustig, ed., Stimmungen im 17. und 18. Jahrhundert, Michaelstein, 1997).

Lindley M., Ortgies I. (2006-11) : “Bach style keyboard tuning” ; (Early Music, 2006-11, p. 613-623).

Marpurg F. 1776 : “Versuch über die musikalische Temperatur” ISBN 0-36408-671-8.

O’Donnell J. 2006 : “Bach's temperament, Occam's razor, and the Neidhardt factor” (Early Music, 2006–11, p. 625-633)

Plomp R. and Levelt W. J. M. 1965 : “Tonal Consonance and Critical Bandwidth”, The Journal of the Acoustical Society of America, 38, 548-560.

Raes G.-W. 1928 : “Kompositie, Inleiding tot de Kompositie, Experimentele Instrumentenbouw, Akoestiek en Klankonderzoek”. (syllabus Hogeschool Gent “School of Arts”) https://www.logosfoundation.org/kursus/index-kursus.html

Rasch R. 1984 : “Approaches to Tuning and Temperament”, Journal of the Acoustical Society of America.

Rayleigh J. 1877-1888 : “The Theory of Sound”

Romieu J. B. 1758 : “Mémoire théorique et pratique sur les systèmes tempérés de musique. Mémoires de l’Académie Royale des Sciences. Paris.

Rossi L. 1666 : ”Sistema musica ouero Musica speculativa. Stampa Episcopala, Perugia Italië.

Sauveur J. 1701 : “”Principes d’ Acoustique et de Musique ou Système Général des Intervalles des Sons. Mémoires de l’Académie. Paris.

Sethares W. 2005 : “Tuning, Timbre, Spectrum, Scale”, Springer, Londen

Sparschuh A. 1999 : “Stimm– Arithmetic des wohltemperierten Klaviers von J. S. Bach” (Deutsche Mathematiker Vereinigung, Jahrestagung 1999, Mainz, S. 154–155).

Spanyi M. 2006 : "Kirnberger's Temperament and its Use in Today's Musical Praxis" (Clavichord international – 11 (2007-5), 1, Seite 15-22).

Stevin S. 1585 : Van de Spiegheling der singconst

Tartini G. 1754 : “Trattato di musica secondo la vera scienza dell’ armonia” (p. 13).

Taylor B. 1715 : “Methodus incrementorum directa et inversa“.

Vallotti F. 1779 (1728) : “Della scienza teorica e pratica della moderna musica” (book 1).

Vallotti F. 1950 : "Trattato della Moderna"Musica"

Verbeken B. 2016 : “Meetkundige Constructies”, p. 21, fig. 12. VUB ;https://we.vub.ac.be/sites/default/files/files/Bachelorproef_II_Brecht_Verbeken.pdf

Van de Heyning P.H. 2019 : Keel-neus-oorheelkunde en hoofd-halschirurgie”. ISBN 9789036820943

von Helmholtz H. 1863 : Die Lehre von den Tonempfinfingen. Braunschweig ; Druck und Verlag von Friedrich und Sohn

Werckmeister A. 1681 : “Orgelprobe”. Theodorus Phil. Calvisius, Buchhändl in Quedlinburg

Werckmeister A. 1686 : “Musicae Hodegus Curiosus”. (ISBN 9783487040806)

Werckmeister A. 1691 : “Musicalische Temperatur”. Theodorus Phil. Calvisius, Buchhändl in Quedlinburg

Werckmeister A. 1698 : “Orgelprobe”. Leipzig, bei Johann Michael Teubner

Zarlino G. 1588 : “Sopplimenti musicali”

Zapf M. 2001 : "Handing down the Tradition: The survival of Bach's Finger Technique in an Obscure Nineteeht-Century Clavier Tutor". (De Clavicoridio V, sept. 2001, p. 39-44)

1“Un bruit qui coûte cher” ; cfr. Blanmont N. , 2012 : "Scènes et coulisses" ; Ed. Versant Sud.

2“Il faut toujours savoir pourquoi”

3Dati due suoni di qualunque strumento musicale, che posa protrarre, e rinforza il suono per quanto tempo si voglia (trombe, corni di caccia, strumenti d'arco, oboe ec.) si ha un terzo suono ; prodotto dall' urto de due volumi di aria mossi dalli due dati suoni.

Nulla importa al presente bisogno fisica del modo, con cui si produce questo terzo suono ; basta il fatto, e questo si ha debito di spiegare.

4Raes G.-W., https://www.logosfoundation.org/kursus/1086.html

5“Mathematics seductively swims below the surface of music.”

6“Wohltemperierung heißt mathematisch=akustische und praktisch=musikalische Einrichtung von Tonmaterial innerhalb der zwölfstufigen Oktavskala zum einwandfreien Gebrauch in allen Tonarten auf der Grundlage des natürlich= harmonischen Systems mit dem Bestreben möglichster Reinerhaltung der diatonischen Intervalle.”

7Das Betragen von herr Marpurgen gegen Ihnen ist verabscheuungswürdig. ….. Dasz meine und meines feel Vaters Grundsäsze antirameauisch sind, können Sie laut sagen

8Wer die Bachische Lehrmethode in der Composition nach ihrem Umfange kennen lernen will, findet sie in Kirnbergers Kunst des reinen Satzes hinlänglich erläutert.

9“Beyde Arten von Instrumenten müssen guttemperirt seyn, indem man durch die Stimmung der Quinten, Quarten, Probirung der kleinen und grossen Tertien und gantzer Accorde, den meisten Quinten besonders so viel von ihrer größten Reinigkeit abnimmt, daß es das Gehör kaum mercket und man alle vier und zwantzig Ton-Arten gut brauchen kan. Durch [9] Probirung der Quarten hat man den Vortheil, daß man die nöthige Schwebung der Quinten deutlicher hören kan, weil die Quarten ihrem Grund-Tone näher liegen als die Quinten. Sind die Claviere so gestimmt, so kan man sie wegen der Ausübung mit Recht für die reinste Instrumente unter allen ausgeben, indem zwar einige reiner gestimmt aber nicht gespielet werden. Auf dem Claviere spielet man aus allen vier und zwantzig Ton-Arten gleich rein und welches wohl zu mercken vollstimmig, ohngeachtet die Harmonie wegen der Verhältnisse die geringste Unreinigkeit sogleich entdecket. Durch diese neue Art zu temperiren sind wir weiter gekommen als vor dem, obschon die alte Temperatur so beschaffen war, daß einige Ton-Arten reiner waren als man noch jetzo bey vielen Instrumenten antrift. ...”

10“Seinen Flügel konnte ihm Niemand zu Dank bekielen; er that es stets selbst. Auch stimmte er so wohl den Flügel als sein Clavichord selbst, und war so geübt in dieser Arbeit, daß sie ihm nie mehr als eine Viertelstunde kostete. Dann waren aber auch, wenn er fantasirte, alle 24 Tonarten sein; er machte mit ihnen was er wollte. ...”

11So zweckmäßig und sicher Bachs Lehrart im Spielen war, so war sie es auch in der Composition. Den Anfang machte er nicht mit trockenen, zu nichts führenden Contrapuncten, wie es zu seiner Zeit von andern Musiklehrern geschah; noch weniger hielt er seine Schüler mit Berechnungen der Tonverhältnisse auf, die nach seiner Meynung nicht für den Componisten, sondern für den bloßen Theoretiker und Instrumentenmacher gehörten.